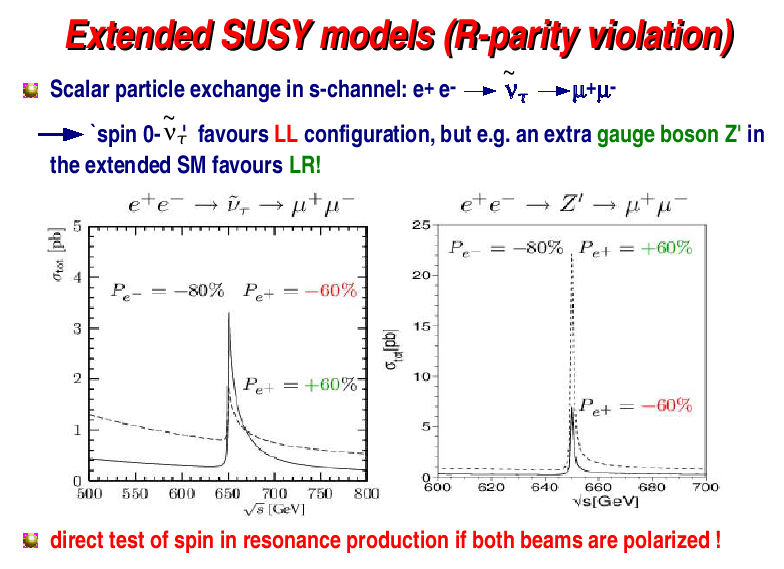
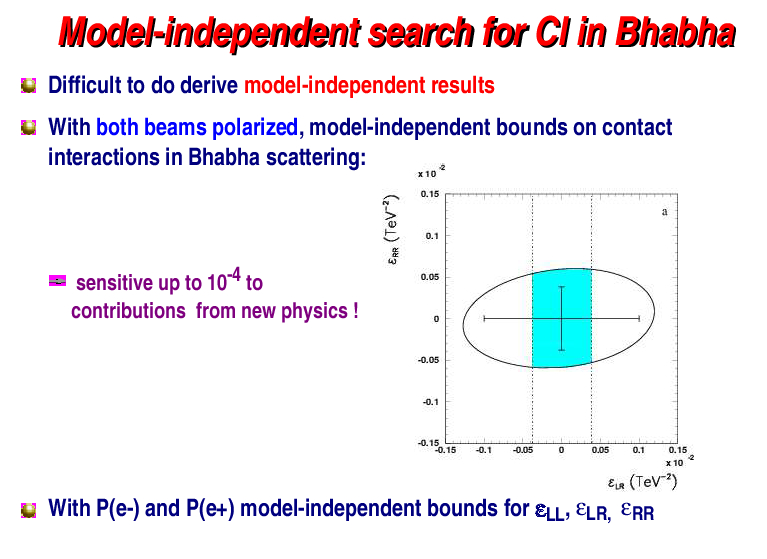
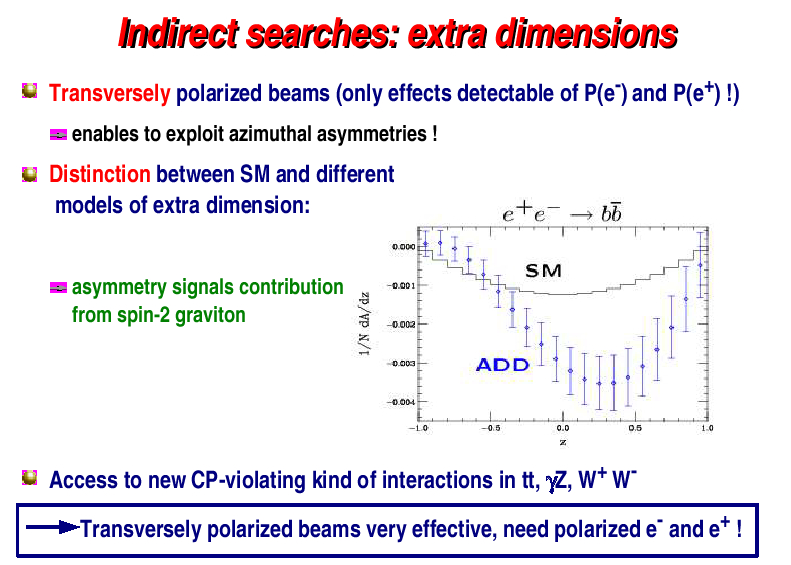
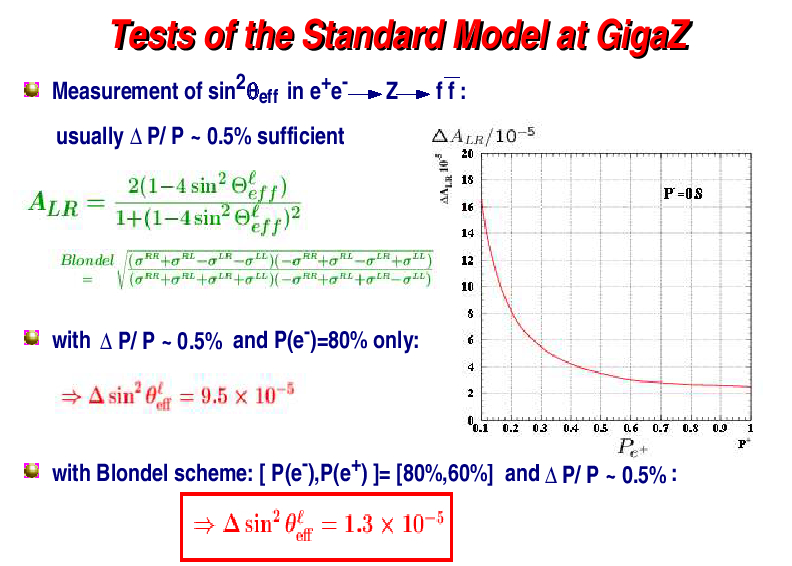
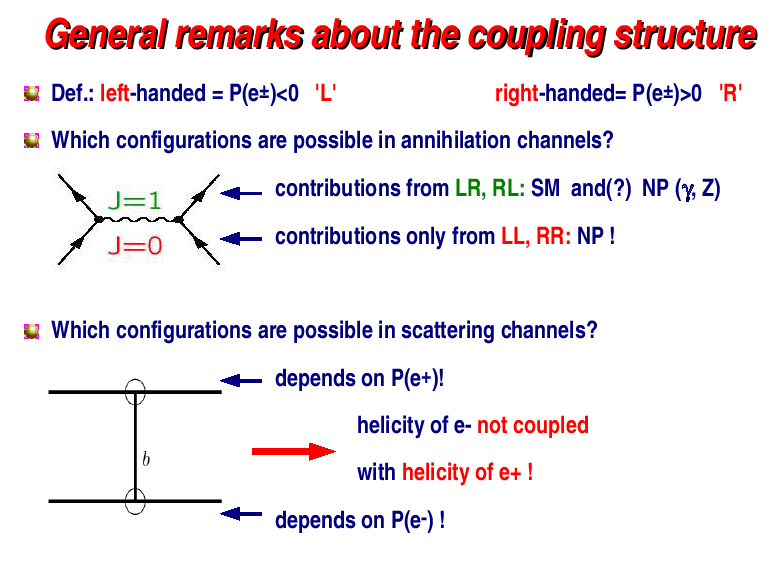
 The dominant processes in e+ e- experiments are annihilation
(s-channel) and scattering (t-channel) processes. In
annihilation diagrams
the helicities of the incoming beams are coupled to each other by the spin of the exchanged particle(s) in
the s-channel (in the Standard Model only J=1 possible).
The dominant processes in e+ e- experiments are annihilation
(s-channel) and scattering (t-channel) processes. In
annihilation diagrams
the helicities of the incoming beams are coupled to each other by the spin of the exchanged particle(s) in
the s-channel (in the Standard Model only J=1 possible).
In t-channel diagrams the helicities of the incoming beams are directly coupled to the chirality of the (new) particles produced. If both beams are polarized, it is possible to adjust independently the polarizations of both beams. This ability provides unique possibilities for probing directly the properties of the produced particles. |