URL: https://www.desy.de/school/school_lab/zeuthen_site/cosmic_particles/glossar/@@siteview
Breadcrumb Navigation
Glossar
S
Scintillator
The Cosmic@Web experiments use so-called organic scintillators. The material they are made of interacts with charged particles. The atoms of the scintillator material are excited by particle impacts. After a very short time, the excess energy is then released again in form of UV light during the transition from the excited state back to the ground state. This light is detected by a photosensor (e.g. a PMT or SiPM), which is connected to the scintillator either directly or via WLS fibers. The photosensor then converts the light into an evaluable electrical signal.
SiPM
The abbreviation SiPM stands for silicon photomultiplier. It is an electronic component with which photons (light particles) can be detected. The signal, which an SiPM delivers, is proportional to the sum of all detected photons. The special characteristic is that the component is composed of several pixels. The pixels themselves are so-called avalanche photodiodes. They are able to detect single photons and convert them into an electrical signal.
Combining several of such pixels in one component - as in an SiPM - offers several advantages over conventional PMTs, which can also be used to detect photons. They enable a very compact design of the detector. The CosMO detectors, for example, use SiPMs with a sensitive surface of only 3x3 mm2. Furthermore, only a low voltage is required for operation, e.g. the CosMOs only require an operating voltage of 70 V. In comparison, an average photomultiplier uses about 800-1800 V.A disadvantage is the noise susceptibility of the SiPMs. They react sensitively to changes in temperature. As a result, the output signal is not only dependent on the amount of incident light, but also on the temperature. Therefore, long-term measurements with SiPMs should be performed at a stable temperature.
The SiPM used in the CosMO detectors is produced by Hamamatsu and called Multi-Pixel Photon Counter (MPPC, product type S10362-33-50C).
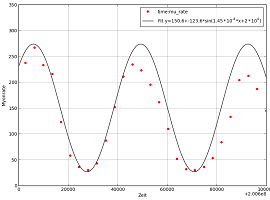
Sine and Cosine Functions
The trigonometric functions sine and cosine and their squares describe mainly periodic processes or the dependence of a physical quantity on the angle. The general form of the sine function is:
- stretch/ compression along the y-axis
- stretch/ compression along the x-axis. This parameter can be determined from the period :
- shift along the x-axis. For a shift in positive x-direction, c is negative, for a shift in negative direction, c is positive.
- shift along the y-axis.
For example, the cosine2 function can be used to describe the zenith angle dependence of the muon flux with the CosMO mill. In Cosmic@Web, a fit function can be inserted directly into the corresponding diagram. The notation in the online analysis tool is as follows: p[0]+p[1]*cos(p[2]*x/180*pi)**2
Where **2 stands for the power. For example, x2 is represented as x**2.
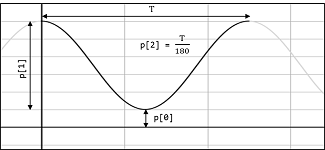 The parameters p[0], p[1] and p[2] refer to the following properties:
The parameters p[0], p[1] and p[2] refer to the following properties:
p[0] - minimum of distribution
p[1] - peak-to-peak amplitude
p[2] - phase
The adjacent diagram shows how to correctly read the parameters: