The basic idea of a halo target is to absorb protons which
leaves the beam core and drift outwards and would get lost anyhow, and
bring them to interaction in the target before they hit any aperture
limitation in the beam tube.
An efficient competition of the target with the collimators, which defines
the aperture of the beam is needed.
The interaction length 
of typical target materials is given in
Tab. 3.
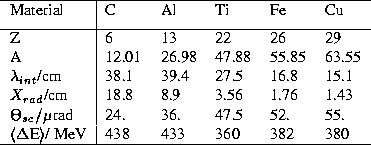
Table 3: Atomic number A, mass Z, interaction length ,
radiation length 
, mean
angular smearing 
and
the mean energy loss 
for various target materials.
A proton has to hit the 
m long target
several hundred times before an interaction occurs.
Diffusion and the scattering in the target are the two
important processes which determines the efficiency of the target.
Fig. 6 shows a simplified sketch of the
beam density with and without
a target at the beam.
Figure 6: Basic impacts of a halo target.
The number N(t) of wire hits after t revolutions can be
estimated by following consideration for a horizontally located
target.
The target wire is located at a position with a betatron amplitude T.
A halo particle with
given betatron amplitude W;SPMgt;T occupy horizontal positions between -W and
+W with 
, depending on the
betatron phase 
, see Fig. 7.
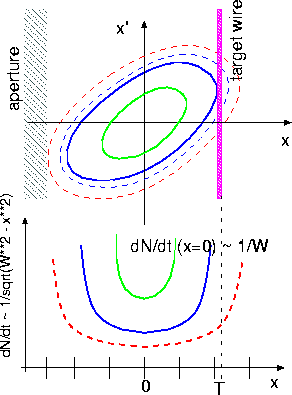
Figure 7: The horizontal phase space with a
target wire at fixed position and the probability to find
a particle at a given x position for particles with various
betatron amplitudes.
Since the phase changes turn by turn
with the tune Q, which is a not a simple rational number,
the phase randomizes after several turns.
The probability that the wire with horizontal width 
(typically 
m) is hit can be approximated by:
Depending on the detailed numbers and the coupling of the horizontal and vertical betatron motion one gets values of several ten-thousand to a few hundred-thousand turns before the proton interact in the wire, i.e. typical times in the order of a second.
Diffusion effects have a similar time scale and it is therefore important
to consider them a little bit more in detail.
The steep increase of the drift velocity 
with the betatron
amplitude W
can be parametrised by:
At a typical position of the target at 4 - 6 beam sigmas
lies between 0.1 and 10 
/sec.
Before a proton gets absorbed it passes 
times through the target and scatters in the target material.
The total angular smearing due to scattering is given by:
Tab. 3 list this number for various materials and the HERA energy of 820 GeV. The scattering leads to an effective blow up of the beam which is determined by an increase of the squared betatron amplitude W:
a number which has to be compared with
beam width 
m.
Multiple scattering amounts therefore to a smearing of the betatron amplitude
by a few which has to be added in quadrature to the betatron amplitude
of the halo particles. The corresponding widening of the beam is one of the
limiting factors to the efficiency of the target. The strong Z dependence
of multiple scattering clearly prefers the use of
light target materials. In addition a small 
function is advantageous
to minimize the widening of the beam.
Particles traverses the target also loses energy. The energy loss of 820 MeV protons per interaction length is summarized in Tab. 3. This energy loss leads to synchrotron oscillation in the longitudinal phase space and together with the non-vanishing dispersion in the target area to deviations from the design orbit in the transverse phase space. Some details will be discussed in section 5.5 in conjunction with the observation of non-bunch correlated interactions.