URL: https://www.desy.de/schule/schuelerlabore/standort_zeuthen/kosmische_teilchen/glossar/@@siteview
Breadcrumb Navigation
Glossar
L
Lineare Funktionen
Lineare Funktionen zeigen proportionale Zusammenhänge. Das bedeutet, dass das Verhältnis von zwei Größen zu einander immer gleich bleibt. Der Funktionsgraph ist also eine Gerade.
Die allgemeinen Form lautet: . Dabei ist die Steigung, berechnet aus 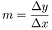 ,
,
und der Schnittpunkt des Graphen mit der y-Achse.
Luftdruckkorrektur
Die Luft zeichnet sich dadurch aus, dass alle Luftteilchen im Raum frei umherfliegen und dabei aneinanderstoßen. Befindet sich Luft in einem Behälter, so stoßen die Luftteilchen auch ständig gegen die Behälterwände und prallen wie Bälle an einer Wand ab. Durch dieses intensive Prasseln der Luftteilchen wirkt eine Kraft senkrecht auf die Behälterwand: Die Luft übt einen Druck aus. Je nachdem ob die Luftteilchen mehr oder weniger Raum für ihre Bewegung haben, ist der Luftdruck gering oder hoch. Das bedeutet, dass bei hohem Luftdruck der Abstand zwischen den einzelnen Luftteilchen kleiner ist. Dagegen ist der Abstand zwischen den Luftteilchen bei niedrigem Luftdruck größer.
Da die kosmischen Teilchen bei ihrem Gang durch die Erdatmosphäre mit den Teilchen der Luft wechselwirken, hat der Abstand zwischen den Luftteilchen und damit der Luftdruck einen Einfluss auf die Anzahl der kosmischen Teilchen, die auf der Erdoberfläche gemessen werden können. Bereits in den 1920er Jahren konnten Physiker experimentell nachweisen, dass bei hohem Luftdruck die Rate kosmischer Teilchen geringer und bei geringem Luftdruck höher ist. Wirklich erklären konnte man diesen Effekt aber erst durch die Entdeckung von Myonen und Pionen viele Jahre später. Wenn Primärteilchen der kosmischen Strahlung mit Luftmolekülen wechselwirken, entstehen neben anderen Teilchen auch geladene Pionen. Pionen zerfallen nach einer extrem kurzen mittleren Lebenszeit in ein Myon und ein Neutrino. Bei niedrigem Luftdruck ist die Dichte der Luft geringer und es ist wahrscheinlicher, dass Pionen zerfallen, bevor sie mit anderen Kernen wechselwirken können. Dies führt zu einer höheren Rate von Myonen, die die Erdoberfläche erreichen.
Um den Zusammenhang zu untersuchen, werden die Daten gefittet. Das bedeutet, dass eine Funktion gesucht wird, die die Datenverteilung am besten beschreibt. Dabei soll die Abweichung (der Fehler) zwischen wahrem, gemessenen Wert und Wert der Funktion möglichst klein sein. Computerprogramme können automatisch den besten Fit mit dem kleinsten Fehler finden. Per Hand ist das zwar auch möglich, aber sehr aufwändig.
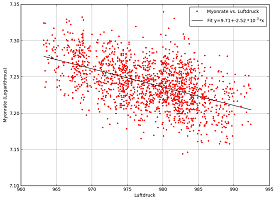
 In der nebenstehenden Abbildung ist als Beispiel die 2013 von der Neumayer Station III gemessene Myonrate in Abhängigkeit des Luftdrucks aufgetragen. Lässt man den Computer nun die Messwerte fitten, findet sich ein exponentieller Zusammenhang zwischen dem Luftdruck und der gemessenen Myonrate. Mathematisch beschrieben wird dieser Zusammenhang mit der allgemeinen Form
In der nebenstehenden Abbildung ist als Beispiel die 2013 von der Neumayer Station III gemessene Myonrate in Abhängigkeit des Luftdrucks aufgetragen. Lässt man den Computer nun die Messwerte fitten, findet sich ein exponentieller Zusammenhang zwischen dem Luftdruck und der gemessenen Myonrate. Mathematisch beschrieben wird dieser Zusammenhang mit der allgemeinen Form
wobei die Myonrate, der Luftdruck und sowie Faktoren sind, die von der jeweiligen Messung abhängen.
Bei vielen Untersuchungen ist es notwendig, die Rate kosmischer Teilchen unabhängig von Luftdruckschwankungen zu untersuchen. Was man macht, ist eine Korrekturfunktion zu suchen, die diese Schwankungen ausgleicht. An dieser Stelle gibt es einen Trick: da das physikalische Problem mathematisch einfacher über einen linearen Zusammenhang zu bearbeiten ist, wird der Logarithmus als Umkehrfunktion der Exponentialfunktion auf die gemessene Myonrate angewendet.
 Durch die so erhaltene Verteilung lässt sich ein linearer Fit der Form
Durch die so erhaltene Verteilung lässt sich ein linearer Fit der Form
legen.
Um nun zu der gesuchten Korrekturfunktion zu gelangen, die auf die experimentellen Daten angewendet werden kann, muss der Anstieg bestimmt werden. Dieser lässt sich aus der nebenstehenden Abbildung formulieren:
Dieser Ansatz wird dann folgendermaßen umgestellt:
wobei der barometrische Koeffizient, die gemessene Myonen-Rate, die korrigierte Myonen-Rate, der gemessene Luftdruck und der Mittelwert des Luftdrucks sind.
Der rechte Teil der Gleichung kann nun als Korrekturfunktion für die in Cosmic@Web zur Verfügung gestellten Teilchenraten genutzt werden. Doch wie sind die einzelnen Paramter und Variablen zu bestimmen?
Schritt 1: Der Luftdruck , auf den normiert werden soll, ist der mittlere Luftdruck des zu untersuchenden Zeitraums, z. B. ein Jahr. Dieser wird als „mean“ in der Legende eines 1D- Histogramms angezeigt.
Schritt 2: Der Anstieg wird von Cosmic@Web automatisch bei der Erstellung des linearen Fits berechnet. Zwar müssen trotzdem Startparameter für die Fitfunktion in der richtigen Größenordnung angegeben werden, der genaue Wert wird dann aber in der Legende angezeigt.
Schritt 3: Schließlich sind die unkorrigierten Teilchenraten im zeitlichen Verlauf darzustellen. Die obige Gleichung ist als Korrekturfunktion für die Teilchenrate anzugeben. Dabei sind für die Parameter und die konkreten, aus den Diagrammen abgelesenen Werte zu verwenden.


 ZUM HERUNTERLADEN
ZUM HERUNTERLADEN