2. Grundlagen
Hier sollen zunächst die Grundlagen der Comptonspektroskopie und speziell des (g, eg)-Koinzidenzexperimentes eingehender vorgestellt werden. Im dritten Abschnitt wird das verwendete Detektorprinzip für die Elektronen, sowie dessen Auswertung beschrieben.
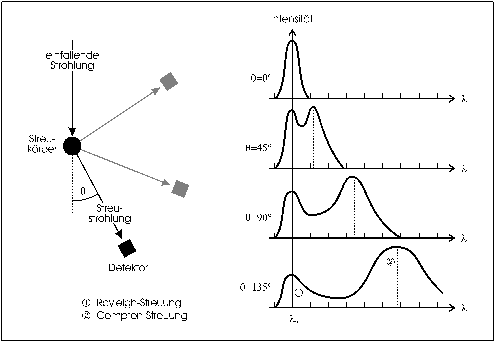
Der 1921 von Arthur Compton beobachtete Effekt beschreibt die Streuung von Licht an ruhenden, nicht gebundenen Elektronen. Betrachtet man das Licht als elektromagnetische Welle, so werden die Elektronen der Probe durch die Welle zu Schwingungen angeregt, deren Frequenz der der Welle entspricht. Die beschleunigten Elektronen senden nun ihrerseits eine elektromagnetische Kugelwelle aus, deren Frequenz von der Bewegung der Elektronen bestimmt wird und somit der der einfallenden Lichtwelle entspricht. Das Licht wird in alle Raumrichtungen gestreut, behält jedoch seine Frequenz bei. Diese Streuung bezeichnet man als Rayleigh-Streuung und war schon länger bekannt. Compton stellte jedoch auch Streulicht mit einer veränderten Frequenz fest, deren Frequenzdifferenz obendrein vom Raumwinkel abhängig war [Com22], wie in Abbildung 1 dargestellt.

Abbildung 1: Schema des klassischen Compton-Experimentes und der Meßergebnisse
Eine Erklärung [Alo92, Hak90] gelingt nur mit dem Teilchenbild des Lichtes. Hierbei ist Licht ein Strom von masselosen Teilchen, den Photonen. Die Streuung resultiert durch die Ablenkung eines Photons nach einem elastischen Stoß mit einem Elektron. Die Gesamtenergie und der Gesamtimpuls beider beteiligten Teilchen müssen vor und nach dem Stoß identisch sein. Wegen des Energieerhaltungssatzes gilt:
![]() . (1)
. (1)
Hierbei ist n die Frequenz des Lichtes vor, n' die nach dem Stoß. Die Ruhemasse des Elektrons ist m0, die des bewegten m. Letztere ist bestimmt durch die Geschwindigkeit v des Elektrons
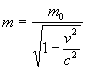 . (2)
. (2)
Setzen wir dies in Formel 1 ein, formen um und quadrieren, erhalten wir
![]() . (3)
. (3)
Um das Photon um q ablenken zu können, muß das Elektron in die unbekannte Richtung F beschleunigt werden. Für die Impulse in x- und y-Richtung schreiben wir also
![]() . (4, 5)
. (4, 5)
Durch Anwenden von sin2F+cos2F=1 eliminieren wir F. Wiederum setzen wir die Beziehung zwischen m und m0 ein, erweitern mit (v-v')2 und bekommen
![]() . (6)
. (6)
Die rechte Seite der Gleichung ist identisch mit dem Ergebnis der Energiebilanz (Formel 3), so daß man die linken Seiten gleichsetzen kann
![]() , (7)
, (7)
und erhält nach Kürzen
![]() . (8, 9)
. (8, 9)
Nach Umrechnung der Frequenz n in die entsprechende Wellenlänge l ist das Resultat
![]() , (10, 11)
, (10, 11)
wobei wir als Vereinfachung die sogenannte Compton-Wellenlänge lC=h/cm0 benutzen.
Die Wellenlängenverschiebung Dl ist also ausschließlich von der Raumrichtung q, in der gemessen wird, abhängig. Der Effekt ist jedoch nur bei relativ kurzen Wellenlängen und damit hohen Energien der Photonen meßbar. Bei niederen Energien, beispielsweise von Photonen im sichtbaren Bereich, absorbiert der Photoeffekt die meisten Photonen, so daß diese nicht zur Comptonstreuung kommen. Bei Energien jenseits 1 MeV überwiegt der Paarbildungs-Effekt [Tau90].
Weiterhin sehen wir, daß die Wellenlängenverschiebung, also die Trennung des durch die beiden Streuarten Rayleigh und Compton erzeugten Signale, bei einem Detektorwinkel von 180° am größten ist.
g, eg)-Experiment
Durch die Bewegung, dem Impuls, der Elektronen in der Probe treten Verbreiterungen des Compton-Peaks in den gemessenen Spektren aus Abbildung 1 rechts auf. Jedes Streuereignis findet mit einem Elektron eines anderen Impulses statt, die resultierende Streurichtung des Photons differiert entsprechend. Der vollständige Stoßprozeß ist in Abbildung 2 schematisch dargestellt.
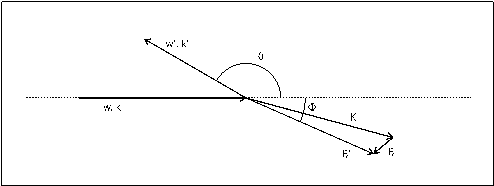
Abbildung 2: Schema der Streugeometrie des Compton-Effektes bei Elektronen mit Impuls
Das einfallende Photon besitzt die Energie w und die Richtung (den Wellenvektor) k. Nach dem Stoß hat sich seine Energie zu w', sein Wellenvektor auf k' geändert. Die Änderung des Wellenvektors, des Impulses des Photons ist K=k-k'. Dieser Impuls wird auf das Elektron übertragen, welches vor dem Stoß den Impuls Pe besaß: Pe'=Pe+K. Der Streuvektor K repräsentiert also den Impulsübertrag. Mißt man Pe' und dazu koinzident die Änderung des Photonenpulses K, erhält man Zugang zum Impuls des Elektrons dieses einen Prozesses vor dem Stoß. Mit einer Vielzahl dieser Messungen läßt sich die Elektronenimpulsdichte statistisch bestimmen [Bel90].
Der verwendete Versuchsaufbau erlaubt jedoch keine genügend genaue Bestimmung der Energie der Rückstoßelektronen. Mit dem verwendeten ortsauflösenden Elektronendetektor kann nur die Richtungskomponente des Impulses bestimmt werden. Die Energie ist indirekt durch die Energieerhaltung unter Vernachlässigung der Bindungsenergie über den Energieverlust der Photonen zugänglich [Kur97]. Die Genauigkeit bei der Messung der Richtung F der Rückstoßelektronen geht direkt als Fehlerquelle in die Elektronenimpulsdichte ein. Man ist also bemüht, diesen Winkel möglichst exakt zu bestimmen. Der Elektronendetektor ist in einzelne Pixel aufgeteilt, die jeweils für eine Raumrichtung zuständig sind. Wenn der Detektor im Abstand l von der Probe entfernt angebracht ist und ein Pixel die Kantenlänge a besitzt, errechnet sich die Standardabweichung sFe für die Fehlerfortpflanzung [Sat97] zu
 . (12)
. (12)
Um die Elektronenimpulsdichte bestimmen zu können, muß jedes einzelne Ereignis ausgewertet und über die Ereignisse eine Statistik geführt werden. Je mehr Ereignisse in diese eingehen, desto höher wird die statistische Genauigkeit. Man versucht also die Rate der Koinzidenzen möglichst zu erhöhen. Die größte Zahl von Comptonereignissen läßt sich unter einem Winkel q von 180° beobachten. Da aus dieser Richtung jedoch der einfallende Photonenstrahl kommt, wählt man einen kleineren Winkel. Bei den aktuellen Messungen wurde ein q von 150° benutzt. Die dazugehörigen Elektronen treten dann im Mittel bei F=11,3° aus. Eine Vergrößerung von q hätte eine Verkleinerung von F zur Folge, der Elektronendetektor läge dann im Strahlgang der ungestreuten Photonen.
Um die im (g, eg)-Experiment erzeugten Rückstoßelektronen nachweisen zu können, werden PIN-Photodioden benutzt. Alternative Prinzipien, wie Gasdrahtkammern oder Vielstreifendetektoren, sind nicht gut für dieses Experiment geeignet. Gasdrahtkammern sind nur schlecht an das Vakuum der Streukammer anzukoppeln, während Vielstreifendetektoren Übersprechen von Streifen zu Streifen zeigen können [Tsc93].
Das Prinzip der Detektion von Elektronen in PIN-Dioden wird in Abschnitt 1 erläutert. Der erzeugte Ladungsimpuls wird dann vorverstärkt (Abschnitt 2) und schließlich zur Signalverbesserung mit einem pulsformenden Hauptverstärker aufbereitet, auf dessen Wirkungsweise in Abschnitt 3 eingegangen wird.
Die Ortsauflösung wird durch die Verwendung mehrerer Einzeldetektoren in einem Array erzielt. Abbildung 3 zeigt das bislang verwendete Array mit Photodioden, die eine aktive Fläche von 10 x 10 mm2 besitzen. Die Mittelpunkte sind jeweils 13 mm voneinander entfernt.
Eine Erhöhung der Winkelauflösung ist entweder durch die Vergrößerung des Abstandes des Detektors von der Probe, oder durch ein Array mit kleineren Diodenflächen möglich. Der von einer Diode gemessene Winkelbereich Dq errechnet sich mit dem Abstand der Dioden b und des Abstandes von der Probe l zu Dq=b/l (q in Radiant, mit der Näherung sina=a für kleine a). Eine Diode ist bei dem obigen Detektor, der in einem Abstand von etwa 1,5 m angebracht ist, für einen Winkelbereich von Dq=0,5° zuständig. Eine Verbesserung der Auflösung geht aber immer mit einer Erhöhung der Pixelzahl einher, damit der vermessene Winkelraum nicht kleiner wird. Werden mehr Pixel verwandt, sinkt andererseits die Zählrate für ein einzelnes Raumwinkelelement und erfordert längere Meßzeiten.

Abbildung 3: Draufsicht des Dioden-Arrays des beim Desy vorhandenen Elektronendetektors in Originalgröße. Die Dioden haben äußere Abmaße von 11 x 11 mm und ihre Mittelpunkte sind jeweils 13 mm voneinander entfernt.
Eine Verbesserung der Akzeptanz des Detektors, und damit der Rate der gemessenen Ereignisse pro Pixel ist durch eine Erhöhung der Flächennutzung f möglich. Die Flächennutzung ist der Quotient von aktiver Fläche zu Gesamtfläche. Hat die aktive Diodenfläche eine Kantenlänge von a und der Abstand der Diodenmitten beträgt b, so ist die Flächennutzung
![]() . (13)
. (13)
Dieser Wert ist bei dem vorhandenen Detektor f=0,59. Es können also nur 59% der Elektronen wirklich nachgewiesen werden.
Hier soll gezeigt werden, welche Vorgänge bei der Detektion in pn-Dioden ablaufen. Danach wird auf die Besonderheiten von PIN-Dioden im Vergleich zu normalen pn-Dioden eingegangen.
Bei pn-Dioden wird der Sperrschicht-Photoeffekt von pn-Halbleiterübergängen ausgenutzt, um Strahlung nachzuweisen. Hierbei wird an die Diode eine Spannung in Sperrichtung angelegt. Diese vergrößert die aufgrund der unterschiedlichen Dotierungen vorhandene Raumladungszone (RLZ). Wird ein Elektron im Bereich der RLZ aus dem Leitungs- in das Valenzband angehoben, so werden das Elektron und das entstandene Loch räumlich durch das elektrische Feld getrennt. Die Bewegung der Ladungsträger im Feld erzeugt einen Influenzstrom, den Photostrom iph. An den Anschlüssen der Diode ist dieser zusammen mit dem Dunkelstrom meßbar. Beschreiben wir den Dunkelstrom nach Shokley, erhalten wir für den gemessenen Strom i
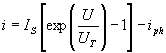 . (14)
. (14)
Der Dunkelstrom ist zeitlich konstant und nur von der Sperrspannung abhängig. Der Photostrom ist jedoch, solange keine konstante Bestrahlung vorliegt, zeitlich variant. Wenn sich Ladungsträger in der RLZ bewegen, ist der Strom meßbar. Erreichen die Ladungsträger den RLZ-Rand, so hört der Strom auf.
Wird ein einzelnes Photon in den Halbleiter gestrahlt, so kann dieses ein Elektron des Valenzbandes anregen (sofern es genug Energie besitzt, damit das Elektron die Bandlücke überqueren kann). Es gibt seine Energie an das Elektron ab (siehe Abb. 4a). Geschieht dies innerhalb der RLZ, kann der Effekt durch den Photostrom nachgewiesen werden. Wenn die Erregung jedoch nicht in der RLZ stattfindet, werden die beiden Ladungsträger nicht getrennt und vernichten sich nach der Ladungsträgerlebensdauer te wieder; insbesondere fließt kein Photostrom.
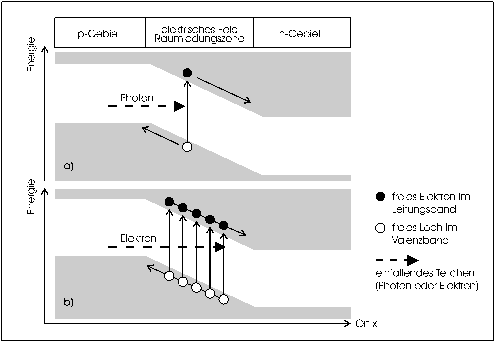
Abbildung 4: Prinzip des Sperrschicht-Photoeffektes in Halbleitern
Ein in den Halbleiter eindringendes Elektron erzeugt eine ganze Reihe von Paaren, deren Anzahl proportional zur Anfangsenergie des einfliegenden Elektrons ist. Es gibt seine Energie sukzessive an Valenzbandelektronen ab, die ins Leitungsband wechseln (Abb. 4b). Befinden sich die Ladungsträgerpaare in der RLZ, erzeugen sie zusammen einen Influenzstrom, dessen Stärke proportional zur Anzahl der Paare ist. Gibt das einfliegende Elektron also seine Energie vollständig und nur an Elektronen in der RLZ ab, so ist die Energie, die es zu Beginn hatte, durch dem Photostrom meßbar.
In normalen pn-Dioden ist die räumliche Ausdehnung der RLZ sehr gering. Typische Werte sind einige wenige µm. Für die vollständige Absorbtion der Energie der einfliegenden Elektronen, die in unserem Fall bei 70 keV liegt, sind jedoch Strecken erforderlich, die mindestens eine Größenordung höher liegen. Eine Vergrößerung der RLZ durch Erhöhung der Sperrspannung ist einerseits durch die Durchschlagfestigkeit begrenzt, und zusätzlich verschlechtert sich das Zeitverhalten durch Diffusionsanteile des Photostroms [Blu95]. Es werden also PIN-Dioden verwendet, die es erlauben, die RLZ durch den kompletten Halbleiter auszudehnen und somit annähernd eine Steigerung der Weite um zwei Größenordnungen bewirken.
Zwischen den n- und p-Gebieten liegt bei diesem Typ von Photodioden eine quasiintrinsische Schicht. Sie wird zumeist aus undotiertem Substratmaterial gebildet und ist entweder schwach n (n-) oder p (p-) dotiert. Ist keine Spannung in Sperrichtung angelegt, bilden sich, wie in Abbildung 5a gezeigt, an den Dotiersprüngen zwei kleine RLZ aus. Mit Sperrspannung vereinigen sich diese jedoch zu einer großen RLZ, die das gesamte intrinsische Gebiet umfaßt (Abb. 5b). Die Kapazität der Diode wird nun auch minimal (vergl. Formel 17).
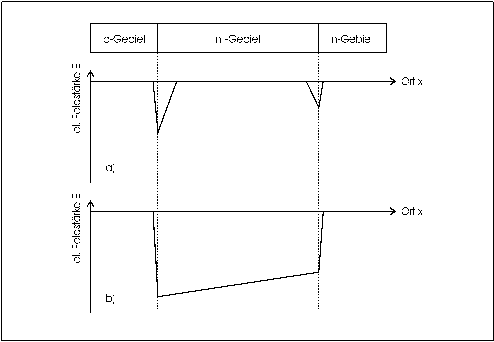
Abbildung 5: Ausbildung des elektrischen Feldes in PIN-Dioden ohne externe Spannung (a) und mit Spannung in Sperrichtung (b)
Die Weite ist in diesem Fall nur von der Dicke der Mittelschicht abhängig, die beim Produktionsprozeß bestimmt werden kann. Im Maximalfall sind die p- und n-Gebiete jeweils von oben beziehungsweise unten in den Halbleiter eindiffundiert. Als intrinsische Schicht und damit RLZ steht dann fast die gesamte Tiefe des Kristalls zur Verfügung. Diese beträgt üblicherweise zwischen 300 µm und 500 µm.
Der von den Photodioden beim Eindringen eines Elektrons erzeugte Ladungspuls soll nun gemessen werden. Das Signal der Diode besitzt eine hohe Impedanz, so daß der nachfolgende Verstärker ebenfalls eine hohe Impedanz besitzen sollte. Ein als Integrierer geschalteter Operationsverstärker (OP) besitzt diese Eigenschaft. Er integriert den schwachen Ladungspuls und erzeugt eine proportionale Spannung mir geringer Impedanz, die leicht weiterverarbeitet werden kann. Durch diese Betriebsart nennt man einen solchen Verstärker auch Ladungs(empfindlicher)verstärker (LeV).
Die Photodiode wird im Betrieb mit einer Gleichspannung zum Aufbau der RLZ versorgt. Damit keine von einem gemessenen Elektron erzeugte Ladung Q über die Diodenspannungsversorgung abfließt, wird diese sehr hochohmig über einen Widerstand RHV angeschlossen. Der Ladungsverstärker soll nur den Ladungspuls erhalten, wird also gleichspannungsmäßig mit einem Kondensator Ck abgekoppelt.
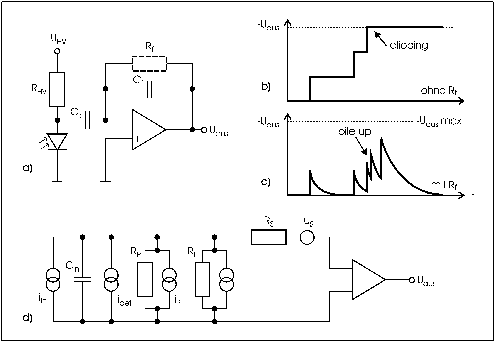
Abbildung 6: Prinzipschaltbild eines Ladungsverstärkers (a) und des Ausgangssignals ohne (b) und mit (c) Entladewiderstand R
f. Teilbild (d) zeigt das Kleinsignalmodell mit eingetragenen Rauschquellen.
Dieser ist direkt mit dem negativen Eingang des OPs verbunden. Der positive Eingang liegt auf Masse. Durch den Kondensator Ck übertragener Strom kann nicht in den hochohmigen Eingang des OPs fließen, sondern gelangt in den Integrationskondensator Cf, der geladen wird. Seine linke Seite liegt quasi an Masse, die gesamte durch die Ladung entstandene Spannung Uaus=-Q/Cf wird am Ausgang meßbar (Abbildung 6a).
Allerdings läuft die Ausgangsspannung selbst ohne Eingangssignal an die Aussteuergrenze (clipping), weil Offsetspannung und Eingangsruhestrom des OP ebenso integriert werden [Kor95]. Dieser Effekt, der auch nach der Integration einiger Eingangspulse auftritt (Abb. 6b), wird durch den Widerstand Rf verhindert (Abb. 6c), der den Kondensator Cf laufend entlädt. Alternative Verfahren sind das rhythmische Entladen des Kondensators durch Belichten des Eingangstransistors des Verstärkers [Gou70] oder Ausnutzen des Leckstroms desselben [Ela72].
Wenn sich Signale häufen, so daß der Kondensator Cf bei einem neuen Puls noch nicht entladen ist, erreicht die Ausgangsspannung höhere Werte als erwartet (pile-up-Effekt in Abb. 6c). Als Grenzfrequenz fpile-up der Ereignisse kann in etwa angesetzt werden
![]() . (15)
. (15)
Bei den bislang verwendeten kommerziellen Verstärkern liegt fpile-up bei 2 kHz.
Der Ladungsverstärker verursacht nur einen Teil des Gesamtrauschens des Detektors. Folgende Effekte verschlechtern die Genauigkeit in der Energiebestimmung; außer Punkt 1 und 2 sind es auch die Ursachen für das Grundrauschen:
1. Schwankung der erzeugten Ladungsträger je Ereignis
2. Schwankung der Nachweiseffizienz
3. Rauchen des Detektorstroms im Volumen
4. Oberflächenrauschen des Detektors
5. Rauschen der Verstärkerelektronik
Hier soll nun auf das Rauschen der Verstärkerelektronik eingegangen werden. Das Kleinsignalmodell des Verstärkers ist in Abbildung 6d dargestellt. Der zu messende, durch ein einfliegendes Elektron erzeugte Strompuls ist iin. Cin ist die Summe der beteiligten Kapazitäten: Detektor-Kapazität Cj, Gate-Source-Kapazität des Eingangstransistors CGS, Integrationskondensator Cf, Koppelkondensator CK und weitere Streukapazitäten CX. Die Rauschstromquelle idet ist die Summe vom Rauschstrom im Detektorsperrstrom id und im Gate-Strom igs des Eingangstransistors. RP repräsentiert den Rückkopplungswiderstand Rf und den Widerstand RHV in der Detektorversorgung RP=Rf//RHV; iP deren Rauschströme. Der Strom il symbolisiert die Leckströme in den verschiedenen Komponenten von Cin und zum Beispiel durch das Platinenmaterial. Rl stellt den dazugehörigen Innenwiderstand dar. Der Serienwiderstand RS wird gebildet durch Reihenschaltung vom Innenwiderstand der Detektordiode und dem Kanalwiderstands des Eingangstransistors; die Rauschspannung uS entsteht über RS. Der Eingangstransistor erzeugt noch eine zusätzliche Rauschspannung uf (Flicker-Noise), die auf Schwankungen der Leitfähigkeit beruht und hier nicht näher betrachtet werden soll.
Von besonderem Interesse ist die Temperaturabhängigkeit der Rauschbestandteile. In [Wei92] ist der Ansatz für die Energieauflösung DE gegeben durch
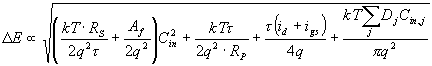 . (16)
. (16)
Hierbei sind k die Bolzmannkonstante, T die absolute Temperatur, q die Elektronenladung und Af die Flicker-Noise-Konstante des Eingangstransistors. Dj sind die Verlustfaktoren der einzelnen Cj. Üblicherweise wird nach dem Ladungsverstärker ein Bandpaßfilter zur Rauschverbesserung eingesetzt, dessen Zeitkonstante hier mit t angesetzt ist.
Die ersten beiden Terme sind stark von Cin abhängig und entsprechen den Serien-Rauschquellen. Die anderen Terme stammen von den Parallel-Rauschquellen. Der erste, dritte und fünfte Term ist linear abhängig von der Temperatur, während id und igs, die den vierten Term bestimmen, sogar exponentiell von T abhängen.
Um ein möglichst geringes Rauschen des Verstärkers zu erzielen, ist Cin also so stark wie möglich zu verkleinern. Ein Kühlen auf 75 K sollte außerdem alle Rauschquellen, außer dem Flicker-Noise, um den Faktor 4 vermindern.
2.3.3. Signalformung und weitere -Verarbeitung
Wollte man die Amplitude direkt am Verstärkerausgang abnehmen, so müßte man die gesamte Signalhistorie berücksichtigen, da der Integrationskondensator zu keiner Zeit vollständig entladen ist. Man verwendet daher Filter, die zeitlich begrenzte Pulse liefern. Wegen des großen Rauschspektrums des Verstärkers kommt hierfür nur ein Bandpaß in Betracht, üblicherweise ein Bessel-Filter [Fal97]. Die Spannungspulse sind hiernach semi-gaußförmig, haben eine definierte Länge und ihr Maximum entspricht der Energie des eingefallenen Elektrons. Die Zeitkonstante t, die beispielsweise bei CR-RC-Bandpässen den Zeitkonstanten der beiden RC-Kombinationen entspricht, muß experimentell optimiert werden, da unbekannte Faktoren wie RS aus Abbildung 6d berücksichtigt werden müssen. Für Elektronendetektion mit PIN-Dioden sind im allgemeinen die besten Zeitkonstanten zwischen 1 ms und 6 ms zu erwarten.
Der für die Versuche eingesetzte Filter, ein pulsformender Verstärker bot nur drei feste Zeitkonstanten von 0,5 ms, 1,5 ms und 3 ms. Die besten Ergebnisse wurden mit 3 ms erzielt.
Bei einem (g, eg)-Experiment wird bei Eintreten eines Photonenereignisses geprüft, ob zugleich ein Signal an einem Pixel des Elektronendetektor anliegt, welches in dem erwarteten Energiebereich liegt. In Abbildung 7 ist ein Spektrum der Elektronenenergien während eines solchen Experimentes zu sehen. Die gesuchten Elektronenereignisse liegen zwischen 50 keV und 100 keV. Im niedrigeren Energiebereich ist das Rauschen zu sehen. Der Peak im hohen Bereich bei 180 keV stammt von Elektronen, die durch den äußeren Photoeffekt aus dem Festkörper geschlagen wurden; sie besitzen bis auf die Bindungsenergie dieselbe Energie wie die eingestrahlten Photonen.
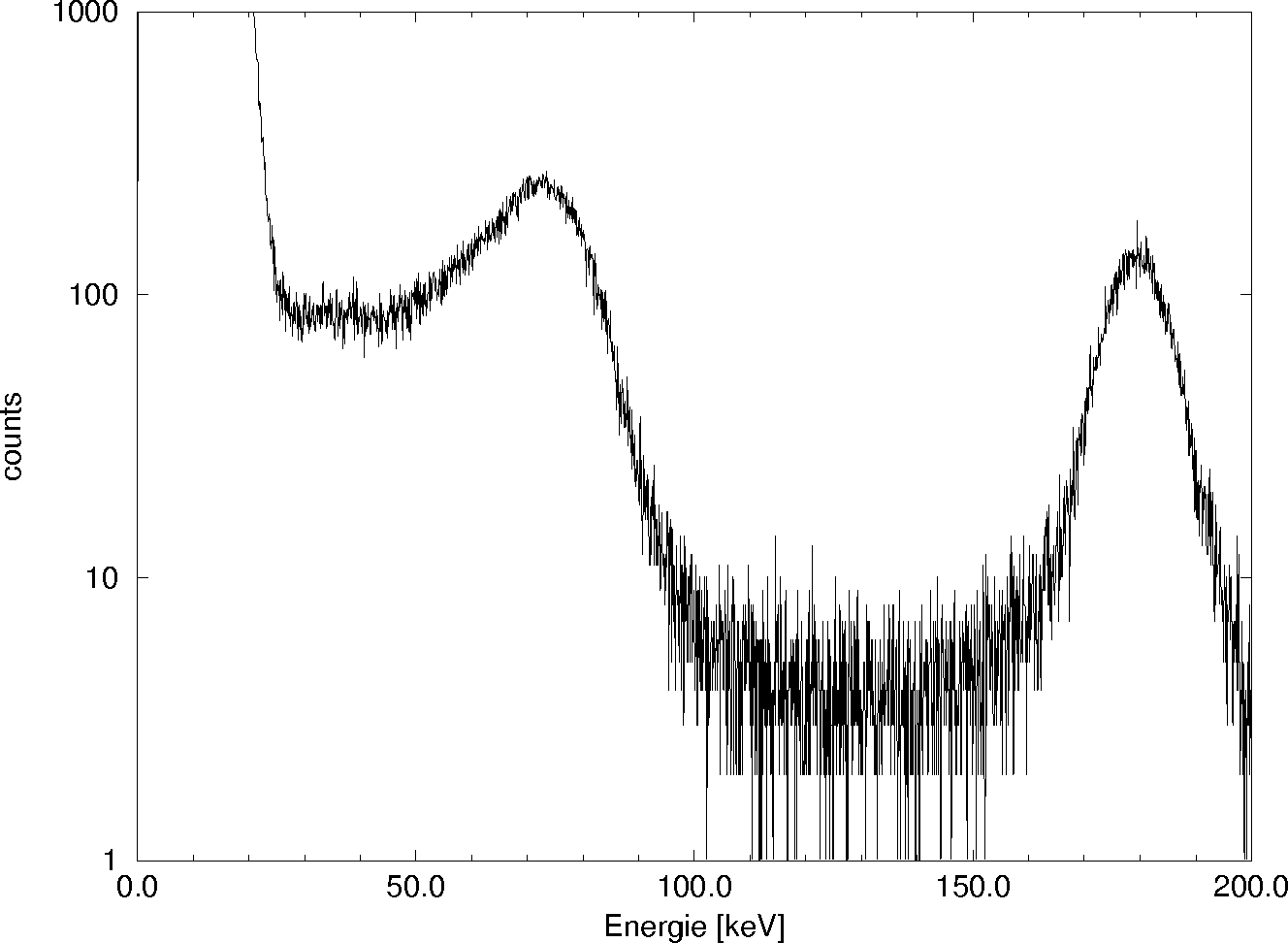
Abbildung 7: Spektrum der Elektronen während einer (
g, eg)-Messung an Kupfer [Sat97b]. Unter 25 keV dominiert das Grundrauschen des Detektors. Der linke Peak bei 70 keV entstand durch Elektronen, die an Comptonprozessen beteiligt waren. Durch vom Photoeffekt ausgelöste Elektronen entstand der rechte Peak.
Um ein solches Spektrum aufzunehmen, benötigt man einen Spitzenwert-Analog-Digitalwandler (Peak-Sensing ADC). Dieser überwacht ständig die Ableitung U' der an seinen Eingang angelegten Spannung U. Hat U' einen Nulldurchgang, so muß ein Spitzenwert (oder ein Sattelpunkt) der Eingangsspannung U vorliegen. Die Höhe der Amplitude von U wird in diesem Augenblick bestimmt, und der Wert digital an ein Histogramm-Analysator (MCA) weitergereicht. Dieser zählt für jeden Spannungswert die Anzahl der Ereignisse. Die Werte werden durch den ADC diskretisiert, üblicherweise mit 13 Bit Auflösung, so daß 8192 Kanäle möglich sind. Die Histogramme können dann in einen Rechner übertragen und weiterverarbeitet werden.
Die Diagramme wie Abbildung 7 besitzen also als Abszisse die Spannung der registrierten Ereignisse, als Ordinate die Anzahl der Ereignisse mit dieser Spannung. Die Spannung repräsentiert die Energie des einfliegenden Elektrons. Die Ordinate repräsentiert somit die spektrale Intensität ¶I·DE/¶E des Elektronenstroms (DE = Energiebreite eines Kanals).
Für die Untersuchungen in dieser Arbeit wurden Elektronenspektren eines radioaktiven ![]() -Präparates aufgenommen. Dieses ermöglicht eine Kalibrierung des Detektors, da die Linien des Spektrums bekannt sind. Weiterhin sind einige der Peaks schmal genug, um die Energieauflösung des Detektors bestimmen zu können. Die Auflösung wird als Halbwertsbreite (FWHM) der Energiepeaks bestimmt - dies ist die Breite des Peaks an der Hälfte seines Maximums. In Abbildung 8 ist dieses im Vergleich mit anderen üblichen Verfahren der Pulsbreitenbestimmung dargestellt.
-Präparates aufgenommen. Dieses ermöglicht eine Kalibrierung des Detektors, da die Linien des Spektrums bekannt sind. Weiterhin sind einige der Peaks schmal genug, um die Energieauflösung des Detektors bestimmen zu können. Die Auflösung wird als Halbwertsbreite (FWHM) der Energiepeaks bestimmt - dies ist die Breite des Peaks an der Hälfte seines Maximums. In Abbildung 8 ist dieses im Vergleich mit anderen üblichen Verfahren der Pulsbreitenbestimmung dargestellt.
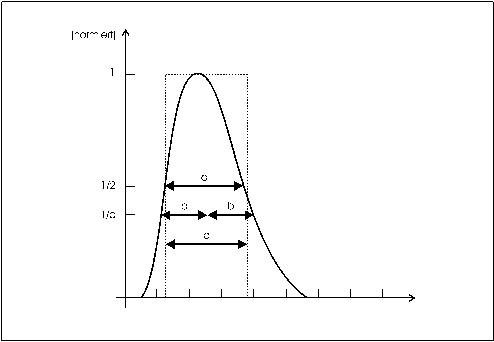
Abbildung 8: Übliche Verfahren zur Bestimmung von Pulsbreiten. Die Halbwertsbreite (a) ist die Breite des Pulses an der Hälfte seines Maximums. Die 1/e-Breite (b) entspricht der halben Breite des Pulses bei 1/e des Maximums. Die Breite des Flächengleichen Rechtecks ist mit (c) dargestellt.
Zurück zu 1. Einführung