Documentation for (outdated) version 16

Note: this documentaion was written for TUnfold version 16. Please consider to use the latest version of TUnfold.

Some documentation is included with the software, such that is becomes part of the Root documentation system. Some additional hints are collected on this web-page. TUnfold is also supported within the RooUnfold package, which provides a common interface to different unfolding methods.

Common problems when using TUnfold

1. Number of bins: you have to use a finer binning in the measured variable as compared to the truth variable. As a rule of thumb, use at least twice the number of bins for the measured variable.

   Example: measure 20 bins and unfold 10 bins. The data histogram has 20 bins. The 2-dimensional histogram has 20x10 bins.

   Note: unfolding with regularisation (τ>0) may still technically work even if the number of measured bins is equal to or less than the number of bins in the "true" variable. However, TUnfold's standard method to estimate the proper value of τ (automated L-curve scan) requires one unfolding step with τ=0 and so this is likely to fail if the number of measured bins is too small.

2. How to unfold Monte Carlo with itself: it is in general a good idea to test the unfolding with Monte Carlo events alone before looking at data. However, the distribution which is unfolded must be statistically independent from the 2-dimensional migration histogram, in order to get meaningful results.

   Example: Split the Monte Carlo into two samples: 90% of the events are used to fill the 2-dimensional histogram, the remaining 10% are used to produce the "data" distribution.

3. Use of the underflow/overflow bins: the underflow and overflow bins of the reconstructed variable have a special meaning.

   Make sure that the underflow/overflow bins are not filled, unless you understand what is going on.

   The meaning of underflow/overflow bins is indicated in the picture below.

   

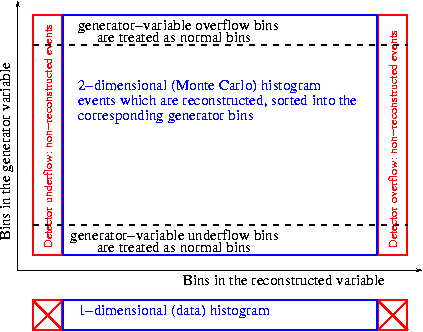
   For the 2-dimensional histogram of migrations, the overflow or underflow bins of the measured variable are used to count the Monte Carlo events which are not reconstructed. The "true" distributions are unfolded using the bins inside the data histograms, but the events in the overflow or underflow bins are used to extrapolate to the full phase-space. This can be understood as an efficiency correction. The underflow and overflow bins of the data histogram are discarded.
   There are also underflow and overflow bins of the "true" variable. These are treated in the same way as the other bins in the "true" variable. This means that the content of the underflow and overflow bins of the "true" variable are unfolded from the data.

   Example: imagine there is some observable P which is non-negative but has no upper bound. However, events with P≥100 are rare.
   • Data histogram filling code:
     // book histogram with 20+1 bins.
     TH1D *data=new TH1D("data","Pdata",21,0.,105.)
     ...
     // fill histogram in event loop
     data->Fill(TMath::Min(Pdata,104.9));
     The data events with Pdata≥100 are all filled into the bin number 21.
   • Migration histogram filling code:
     // book histogram with 20+1 times 10 bins
     TH2D *migration = new TH2D("migration","xdata vs xgen",21.,0.,105.,10,0.,100.);
     ...
     // fill histogram in event loop
     if(isReconstructed) migration->Fill(TMath::Min(Pdata,104.9),Pgen);
     else migration->Fill(-1.,Pgen);
     The events with Pdata≥100 are filled into the bin number 21.
     The events with no reconstruction are filled in the underflow bin.
     For the generated variable, the events with Pgen≥100 end up in the overflow bins of the y-axis.
   As a result, 11 bins are unfolded (10 bins plus one overflow bin in Pgen), using the 21 data bins in Pdata. The unfolded distribution in Pgen is corrected for effciency losses, using the non-reconstructed events as stored in the underflow bin.

TUnfold error messages

It is wise to check the warning and error messages. Make sure root is configured properly to print warning messages when using TUnfold.
Only those errors appearing in the most recent TUnfold version are documented below.
For messages not documented below please contact the author

Level	Source	Message	Comment
Warning/Error	TUnfold	too few (ny=%d) input bins for nx=%d output bins	Reliable unfolding requires a finer binning in the reconstructed variable as compared to the "truth" variable
Fatal	InvertMSparse	InvertMConditioned(full matrix) failed	One of the matrices in your problem has a rank deficit. The most common mistake is to have to few bins in the reconstructed variable and τ=0. Another (rare) possibility is that the covariance matrix for the measured variable can not be inverted.
		InvertMConditioned failed (part of matrix)
		InvertMConditioned failed (full matrix)
Error		inversion failed (diagonal matrix) nerror=%d
		inversion failed (diagonal part) nerror=%d
Warning/Info	TUnfold	%d regularisation conditions have been skipped	Some truth bins of the migration matrix are not populated. Maybe this happened on purpose (overflow/underflow bins).
Warning	SetInput	%d input bins have zero error, 1/error set to %lf.	Sometimes there are data bins with error=0 (for example, if there is no data event). These bins can not be used, unless 1/error>0 is specified.
		%d input bins have zero error, and are ignored.
Info/Warning	TUnfold	the following output bins are not connected to the input side %s	Sometimes there are "truth" bins not connected to any of the data bins (before or after removing data bins with error=0). Such "truth" bins are automatically excluded from the unfolding. In many cases the bins are left empty on purpose (underflow/overflow bin)
	SetInput	%d output bins are not constrained by any data.
		output bin %d depends on ignored input bins %d ... %d
Error	AddSysError	Source %s given twice, ignoring 2nd call.	Systematic error and background sources must have names which are unique
	SubtractBackground
Error	AddSysError	source %s has no influence and has not been added.	Did you provide an empty histogram?