Inelastic Electroproduction of Charmonium

Figure: Differential cross sections a) $d\sigma / dQ^2$ and c) $d\sigma /dp_{t,\psi }^{*2}$ and the corresponding ratios of data to theory (b and d). The data from H1 [30] are compared with the NRQCD calculation [193] (CO+CS, dark band) and the color-singlet contribution [193] (CS, light band).

The analysis of leptoproduction at finite $Q^2$ has experimental and theoretical advantages in comparison with the analysis of photoproduction. At high $Q^2$, theoretical uncertainties in the models decrease and resolved-photon processes are expected to be negligible. Furthermore, the distinct signature of the scattered lepton makes the inelastic process easier to detect. However, due to the steeply falling $Q^2$ dependence the data are more limited statistically.

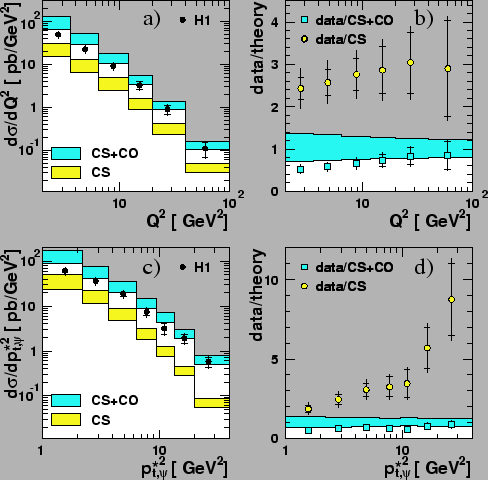
The cross section for $J/\psi$ production in deep-inelastic $ep$ scattering at HERA was calculated in the NRQCD factorization approach at leading order in $\alpha_s$ taking into account diagrams of the type `` $2\rightarrow 2$'' [193] using the matrix elements as determined in [183] and the MRST98LO [73] and CTEQ5L [72] parton distributions. In fig.45, the results of this calculation are plotted as a function of $Q^2$ and $p^{*2}_{t,\psi}$, along with the H1 data [30]. The NRQCD results that are shown in fig.45 include the contributions from the color-octet channels $^{3}\!S_1$, $^{3}\!P_{J=0,1,2}$, $^{1}\!S_0$, as well as from the color-singlet channel $^{3}\!S_1$. The contribution of the color-singlet channel is also shown separately. The values of the NRQCD matrix elements were determined from the distribution of transverse momenta of $J/\psi$ mesons produced in $p\bar{p}$ collisions [183]. The bands include theoretical uncertainties, which originate from the uncertainty in the charm-quark mass $m_c=1.5\pm0.1$ GeV, the variation of renormalization and factorization scales by factors 1/2 and 2, and the uncertainties in the NRQCD matrix elements, all of which result mainly in normalization uncertainties that do not affect the shapes of the distributions.

Figure: Differential cross section $d\sigma /dz$ a) without and b) with a cut on $p^{*2}_{t,\psi }>1$ GeV. The data from ZEUS [33] and in b) also H1 [30] are compared with the NRQCD calculation [193] (CS+CO, open band), the color-singlet contribution (CS, shaded band), with a prediction in the $k_t$ factorization approach assuming the CSM [190] (dotted line) and with the Monte Carlo generator CASCADE (dash-dotted line).

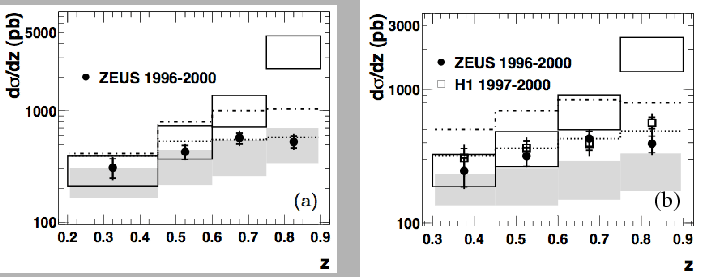Figure 46 shows the differential electroproduction cross sections for $J/\psi$ mesons from ZEUS [33] and H1 [30] as function of $z$. The data are compared with predictions in the framework of NRQCD [193] and also with predictions in the $k_t$ factorization approach in which only the color-singlet contribution (CS) is included [104,190]. The uncertainties in the NRQCD calculations are indicated in fig.46 as bands. The agreement with the color singlet model (CS), seen in fig.46a, deteriorates when the cut $p_{t,\psi}^{*2}>1$ GeV is applied (fig.46b). This cut is justified, however, as towards small $p_{t,\psi}^{*2}$, perturbation theory becomes increasingly unreliable due to collinear singularities for the contributions $e+g \rightarrow e+c\bar{c}[n]+g$ with $n$= $^{1}\!S_0^{(8)}$ and $^3\!P_J^{(8)}$ [193].