URL: https://www.desy.de/school/school_lab/zeuthen_site/cosmic_particles/glossar/@@siteview
Breadcrumb Navigation
Glossar
A
Atmospheric Pressure Correction
As they pass through the Earth's atmosphere, cosmic particles interact with particles in the air. Therefore, the distance between the air particles and thus the air pressure has an influence on the number of cosmic particles that can be measured on the Earth's surface. Back in the 1920s, physicists were able to prove experimentally that the rate of cosmic particles is lower at high atmospheric pressure and higher at low atmospheric pressure. However, this effect could only really be explained many years later after the discovery of muons and pions. When primary particles of cosmic radiation interact with air molecules, charged pions are created along with other particles. Pions decay after an extremely short average lifetime into a muon and a neutrino. At low atmospheric pressure, the density of the air is lower and it is more likely that pions decay before they can interact with other nuclei. This leads to a higher rate of muons reaching the earth's surface.
In order to investigate the correlation, the data is fitted. This means that we seek a function that describes the data distribution best. The deviation (the error) between the true measured value and the value of the function should be as small as possible. Computer programs can automatically find the best fit with the smallest error. Therefore, it varies the variables of the mathematical formula in a way that it results in the best description of the experimental data. This is also possible by manual means, but it is very time-consuming.
 The figure on the right shows the muon rate versus the atmospheric pressure measured by the Neumayer Station III in 2013. The dark blue line is a least squares fitting of the data distribution. It shows an exponential dependence which can be described mathematically with this formula:
The figure on the right shows the muon rate versus the atmospheric pressure measured by the Neumayer Station III in 2013. The dark blue line is a least squares fitting of the data distribution. It shows an exponential dependence which can be described mathematically with this formula:with the muon rate, the atmospheric pressure and and factors depending on the measurement.
Every investigation of cosmic particle rates has to consider variations of the atmospheric pressure. To correct this effect, one has to estimate the dependence of the particle rate on the atmospheric pressure and then apply a correction function. The procedure to estimate this correction function can be simplified by fitting a linear function. The necessary linear relation can be obtained by applying the logarithm of the particle rate versus atmospheric pressure as shown in the second figure.
 Now, the experimental distribution can be described by a linear function:
Now, the experimental distribution can be described by a linear function:
In order to get to the needed correction function, which can be applied to the experimental data, the slope must be determined. For this, the adjacent figure is used:
From this relation the correction function can be derived:
The right part of the equation can now be used as a correction function for the particle rates provided in Cosmic@Web. But how can the individual parameters and variables be determined?
Step 1: The value is the average atmospheric pressure of the investigated period of time. It is displayed as "mean" in the legend of a 1D histogram.
Step 2: In Cosmic@Web the linear fit function and the start parameters have to be defined. Then the slope is fitted automatically and the result is shown in the legend of the log(muon rate) vs air pressure diagram.
Step 3: The corrected particle rate is obtained by setting the correction function into the field “Correction Function for y-Variable” of Cosmic@Web.
Avalanche Photo Diode
An avalanche photodiode is an electrical component that can detect photons and convert them into a measurable current by amplification. If several avalanche photodiodes are connected together, this is called SiPM.
The structure of an avalanche photodiode is similar to that of an ordinary photodiode. The main difference is the insertion of an additional p-layer, which allows the amplification of the signal like an avalanche. An avalanche photodiode consists of a layer sequence p-i-p-n. The individual semiconducting layers each have special properties:
p-layer: Region with free, positive charge carriers (also called holes or defect electrons). The material has been mixed (doped) with foreign atoms, which have a smaller number of outer electrons. As a result, not all bonds are occupied and positive gaps remain in the semiconductor.
n-layer: In contrast to the p-layer, more free electrons are present in this region due to doping. The material is enriched with foreign atoms that have one more outer electron. Thus, an additional, mobile electron is available in the crystal structure of the semiconductor.
i-layer: intrinsic or intrinsically conductive layer. Due to lattice defects, weakly bound electrons are present. Photons with sufficient energy can release these electrons (internal photoelectric effect). These electrons can then move freely in the material.
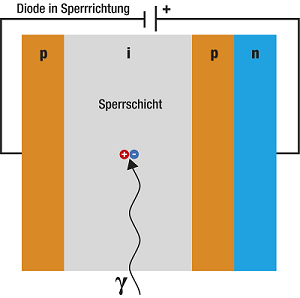
Basically, the measurement starts with the absorption of photons in the i-layer. If a photon hits this layer, electrons are released from the solid lattice structure by the internal photoelectric effect. This results in electron-hole pairs.
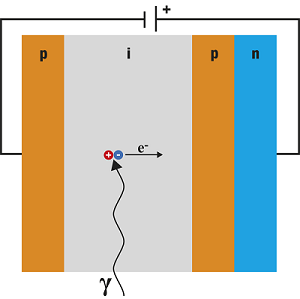
Due to the additionally inserted p-layer, a p-n junction with very high electrical fields is created. The free electrons in the i-layer thus move towards the p-n layer.
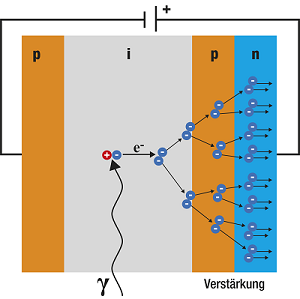
The electrons are strongly accelerated and secondary electrons are produced by impact ionization. These electrons are then accelerated again and in turn produce further electrons.
This avalanche-like generation of secondary electrons in avalanche diodes enables the detection of individual photons. This is not possible with conventional diodes.


