Results to compare for CSR benchmarking
from CSR Workshop 2002
This is an updated version of parameters we want to compare among the various codes. In
the following 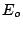 is the beam initial total energy (it is assumed that the beam momentum
is the beam initial total energy (it is assumed that the beam momentum
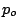 is
is
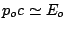 ),
), 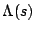 stands for the charge distribution along the bunch
with
stands for the charge distribution along the bunch
with
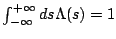 .
Given the longitudinal csr-induced field
.
Given the longitudinal csr-induced field
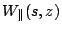 along the bunch at a given
position
along the bunch at a given
position 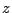 of the beamline, we define the accumulated energy loss (from the beamline entrance
to
of the beamline, we define the accumulated energy loss (from the beamline entrance
to 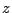 ) as:
) as:
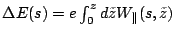 .
.
- plot of
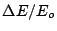 vs
vs 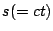 along the bunch and accumulated
over the whole chicane (i.e. downstream of the 2 m drift). From this accumulated wake, compute
the average and rms energy loss defined as:
along the bunch and accumulated
over the whole chicane (i.e. downstream of the 2 m drift). From this accumulated wake, compute
the average and rms energy loss defined as:
and
conventions: particles with 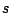 -coordinate
-coordinate 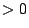 belong to the tail. The units
are:
belong to the tail. The units
are: 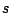 in
in 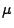 m, and
m, and 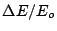 in %.
in %.
- when available: plot of transverse kick (in the bending plane) purely due to the
transverse CSR forces vs
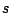 accumulated over the whole chicane.
From this accumulated transverse kick, compute the average and rms transverse kick:
accumulated over the whole chicane.
From this accumulated transverse kick, compute the average and rms transverse kick:
and
where
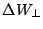 stands for the transverse component of the CSR-induced field.
stands for the transverse component of the CSR-induced field.
conventions: The unit for 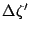 is
is 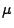 rad.
rad.
- Plot of
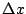 and
and 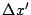 vs
vs 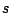 . The quatities
. The quatities 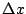 and
and 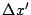 are the changes in position and angle, due to CSR, accumulated over the whole chicane (i.e. downstream of the
2 m drift). Similarly to (1) and (2) compute the mean and rms for
are the changes in position and angle, due to CSR, accumulated over the whole chicane (i.e. downstream of the
2 m drift). Similarly to (1) and (2) compute the mean and rms for 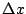 and
and 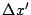 .
.
conventions: The units are: 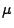 rad for
rad for 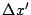 and
and 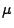 m for
m for 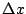 .
.
- Plot temporal distribution at the end of the chicane (units are kA vs
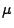 m (again
m (again
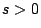 corresponds the bunch tail). Comment as to whether the
corresponds the bunch tail). Comment as to whether the 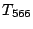 contribution
is included.
contribution
is included.
- Plot of the normalized slice emittance
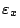 versus
versus 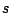 computed at the end
of the beamline (suggestion use 1
computed at the end
of the beamline (suggestion use 1 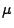 m bin).
m bin).
conventions: Units are mm-mrad for emittance and 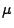 m for
m for 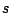 .
.
ASCII format request
In order to generate plots that superimpose the results of the various codes you should
provide the ASCII files:
- item (1) (3) and (4) can be gathered in a 3-column file whose nomenclature is:
column 1: 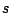 in
in 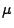 m (
m (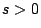 corresponds to tail),
corresponds to tail),
column 2: 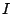 in kA,
in kA,
column 3: 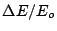 accumulated over the whole chicane in %.
accumulated over the whole chicane in %.
- item (2) should be provided in a separated 3-column file:
column 1: 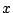 in
in 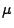 m,
m,
column 2: 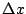 in
in 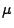 m,
m,
column 3: 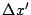 in
in 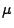 rad.
rad.
- item (5) should be provided in a separate 2-column file:
column 1: 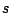 in
in 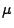 m, (center of the bin within which emittance is computed,
m, (center of the bin within which emittance is computed,
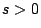 corresponds to tail),
corresponds to tail),
column 2: 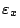 in mm-mrad.
in mm-mrad.
Last updated
2002-02-06
![]() is the beam initial total energy (it is assumed that the beam momentum
is the beam initial total energy (it is assumed that the beam momentum
![]() is
is
![]() ),
), ![]() stands for the charge distribution along the bunch
with
stands for the charge distribution along the bunch
with
![]() .
Given the longitudinal csr-induced field
.
Given the longitudinal csr-induced field
![]() along the bunch at a given
position
along the bunch at a given
position ![]() of the beamline, we define the accumulated energy loss (from the beamline entrance
to
of the beamline, we define the accumulated energy loss (from the beamline entrance
to ![]() ) as:
) as:
![]() .
.
![\begin{displaymath}
\sigma_{\Delta E/E_o } = \left[ \int_{-\infty}^{+\infty} ds ...
...ngle \Delta E/E_o \rangle \right)^2
\Lambda (s) \right]^{1/2}
\end{displaymath}](img12.gif)
![]() -coordinate
-coordinate ![]() belong to the tail. The units
are:
belong to the tail. The units
are: ![]() in
in ![]() m, and
m, and ![]() in %.
in %. ![\begin{displaymath}
\sigma_{\zeta ' } = \left[ \int_{-\infty}^{+\infty} ds
\lef...
...lta W_{\perp}/E_o \rangle \right)^2
\Lambda (s) \right]^{1/2}
\end{displaymath}](img17.gif)
![]() is
is ![]() rad.
rad.