Orbit Correction Basics

Orbit correction is one of the most fundamental processes used for beam control in accelerators. Whether steering beams into collision for high-energy physics, steering photon beams in a synchrotron light source or locating beam on target in a medical application, it is essential to control the beam trajectory. This section investigates closed orbit control for storage ring applications. Extension to steering in transport lines requires only minor modification.

Corrector-to-BPM Response Matrix

The corrector-to-BPM response matrix is an vital piece of information for both orbit control and optics analysis. The response matrix can either be calculated (beta function theory or numerical 'tracking' solutions) or measured directly on the accelerator. The basic format of the response matrix equation is

x = Rq

Where column vector x contains the orbit shift produced by incremental changes in the corrector magnets, q. The response of BPMS to the corrector magnets is contained in R.

An accelerator with m-BPMS and n-correctors produces an m x n dimensional response matrix. It is worth noting that the response matrix is really a sampled version of a continuous function that describes the effect of dipole perturbations at all points in the storage ring on all other points in the storage ring. The linear response of a single dipole perturbation is the well-known closed orbit formula:

In some sense, the closed orbit formula can be thought of as the Greens function or impulse response to a d-function corrector impulse. The impulse is in position, not time.

We often work with differential orbit and corrector changes rather than the absolute orbit and corrector values. The process of orbit control involves defining a differential orbit vector x and solving for the set of differential correctors, q.

Linear Transport Theory (R₁₂ Parameters)

From linear transport theory for a transmission line, particle position and angle evolve as

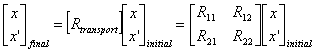
Where R_transport is a 2 x 2 transport matrix. The full 6 x 6 transport matrix includes motion in both transverse planes and in the longitudinal plane. The elements describe beam motion at the i^th BPM (x) in response to a corrector kick at the j^th corrector position (x'). Each element of our 'response matrix' is also an R₁₂ element of a transport matrix connecting corrector kicks to BPM readings but in this case for the closed orbit, not an open transmission line. The reason for using the R₁₂ elements is that we can physically 'kick' with corrector magnets (x') and 'observe' position at BPM sites (x). Throughout this course, we will use ‘q’ for the angular deflection x' imparted by correctors.

Units

In MKS each element of the response matrix has physics units of m/radian, equivalently mm/mrad. It is not uncommon to make mistakes mixing mm/radian or m/mrad when trying to keep the units for the orbit and corrector vectors consistent.  For online applications, the response matrix can have hardware units such as mm/amp, mm/bit, volt/bit, etc. The trick is to keep units consistent. In the orbit control section of this course we use mm/mrad exclusively.

Orbit Correction Algorithms

 Throughout the years, many orbit correction schemes have been devised. This course is concerned with the SVD approach presently in use at many accelerator laboratories worldwide.

In principle, orbit correction seeks to invert the response matrix equations:

x = Rq

q = R^-1x

When a BPM is malfunctioning, not used in the problem, or requires weighting, we strike out or weight the corresponding rows of x and R. A similar process is used for corrector magnets and the columns of R and the rows of q.

1. Harmonic correction – the orbit is decomposed onto a sinusoidal set of basis functions and each component is corrected independently. This method has a solid physical basis because the orbit typically contains strong sinusoidal harmonic components centered near the betatron tunes.

2. Most effective corrector (MICADO) – the Householder transformation is used to find the most effective corrector. After each correction cycle, the next most effective corrector is found. Since corrector magnets produce strong harmonics centered near the betatron tunes, MICADO has proven and effective means to correct global orbit distortions.

3. Eigenvector correction – the orbit is decomposed onto a set of eigenvectors for the response matrix. Since the response matrix contains significant structure near the betatron tunes, the dominant eigenvectors have sinusoidal structure near the betatron tunes. Similar to harmonic correction, the operator can select specific components for correction. The drawback of the eigenvector correction technique is that it requires a square response matrix.

4. Least-squares – when the number of BPM readings exceeds the number of corrector magnets the response matrix becomes 'tall' (more rows than columns). In this case least squares or weighted least-squares can be used to solve for the corrector pattern. Weighting of individual rows of R corresponds to weighting individual BPMS.

5. Singular value decomposition – singular value decomposition performs the same functions as eigenvector or weighted least square corrections but is much more general, mathematically manageable, and numerically robust. In particular, where least-squares breaks down (non-invertible matrix R, singular value decomposition and the associated psuedoinverse produce the full set of eigenvector/eigen value pairs found in the general theory of linear algebra.

6. Constrained problems – Lagrange multipliers and linear programming techniques have been used to constrain errors in the solution vector and corrector magnet strengths. This is a proven, yet still active field of research.

Global and Local Orbit Correction

Global orbit correction refers to calculations that bring the global closed orbit to a desired position. A global orbit correction usually involves many BPMS and corrector magnets distributed throughout the storage ring. The desired orbit may be the 'golden' orbit used for operations or a variant for experimental purposes.

Local orbit corrections or 'bumps' attempt to move the beam orbit in a restricted region. The smallest 'bump' is a 2-corrector bump when the magnets separated by 180 degrees in betatron phase. Otherwise 3 correctors are required to 'close the bump'. In terms of degrees of freedom, in a 3-magnet bump the first magnet deflects the beam and the next two are used to correct position and angle. Three magnet bumps are popular because the analytical solution can be written in terms of beta function parameters. Pure position and angle bumps require four magnets (two to establish position/angle, two to restore position/angle).

Typical Orbit Correction Algorithm

            1. establish reference orbit (beam based alignment)

            2. measure response matrix

            3. select BPMs, correctors and weights and number of singular values

            4. measure actual orbit - check for bad readings

            5. compute difference orbit

            6. compute corrector strength from Dq=R^-1Dx

            7. check for corrector currents in range

            8. apply corrector currents

Least Squares Fitting

Least-squares fitting is common in experimental physics, engineering, and the social sciences. The typical application is where there are more constraints than variables leading to 'tall' rectangular matrices (m>n). Examples from accelerator physics include orbit control (more BPMS than correctors) and response matrix analysis (more measurements in the response matrix than variables).

The simplest linear least-squares problem can be cast in the form

            Ax=b

Where we look to minimize the error between the two column vectors Ax and b. The matrix A is called the design matrix. It is based on a linear model for the system. Column vector x contains variables in the model and column vector b contains the results of experimental measurement. In most cases, when m>n (more rows than columns) Ax does not exactly equal b, i.e., b does not lie in the column space of A. The system of equations is inconsistent. The job of least-squares is to find an ‘average’ solution vector  that solves the system with minimum error. This section outlines the mathematics and geometrical interpretation behind linear least squares. After investigating projection of vectors into lower-dimensional subspaces, least-squares is applied to orbit correction in accelerators.

Vector Projection

We introduce least squares by way projecting a vector onto a line. From vector calculus we know the inner or 'dot' product of two vectors a and b is

= a^Tb = a₁b₁ + a₂b₂ + … + a_nb_n = |a||b|cosq

Where q is the angle at the vertex the two vectors. If the vertex angle is 90 degrees, the vectors are orthogonal and the inner product is zero.

Referring, the projection or perpendicular line from vector b onto the line a lies at point p. Geometrically, the point p is the closest point on line a to vector b. Point p represents the 'least-squares solution' for the 1-dimemsional projection of vector b into line a. The length of vector b – p is the error.

Defining  as the scalar coefficient that tells us how far to move along a, we have

p= a

Since the line between b and a is perpendicular to a,

so

or

In words, the formula reads

            'take the inner product of a with b and normalize to a²'.

The projection point p lies along a at location

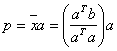
Re-writing this expression as

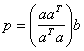
Isolates the projection matrix, P = aa^T/a^Ta. In other words, to project vector b onto the line a, multiply ‘b’ by the projection matrix to find point p=Pb. Projection matrices have important symmetry properties and satisfy Pⁿ=P – the projection of a projection remains constant.

Note that numerator of the projection operator contains the outer product of the vector ‘a’ with itself. The outer product plays a role in determining how closely correlated the components of one vector are with another.

The denominator contains the inner product of a with itself. The inner provides a means to measure how parallel two vectors are ().

MATLAB Example – Projection of a vector onto a line

>>edit lsq_1

Multi-Variable Least Squares

     We now turn to the multi-variable case. The projection operator looks the same but in the formulas the column vector 'a' is replaced with a matrix 'A' with multiple columns. In this case, we project b into the column space of A rather than onto a simple line. The goal is again to find  so as to minimize the geometric error E = |A – b|² where now  is a column vector instead of a single number. The quantity A is a linear combination of the column vectors of A with coefficients ₁, ₂, …_n. Analogous to the single-parameter case, the least-squares solution is the point p=A closest to point b in the column space of A. The error vector b-Ais perpendicular to that space (left null space).

The over-constrained case contains redundant information. If the measurements are not consistent or contain errors, least-squares performs an averaging process that minimizes the mean-square error in the estimate of x. If b is a vector of consistent, error-free measurements, the least-squares solution provides the exact value of x. In the less common under-constrained case, multiple solutions are possible but a solution can be constructed that minimizes the quadradic norm of x using the pseudoinverse.

There are several ways to look at the multi-variable least-squares problem. In each case a square coefficient matrix A^TA must be constructed to generate a set of normal equations prior to inversion. If the columns of A are linearly independent then A^TA is invertible and a unique solution exists for .

1) Algebraic solution – produce a square matrix and invert

            A = b

            A^TA = A^Tb                           (normal equations for system Ax=b)

 = (A^TA)^-1A^Tb

The matrices A^TA and (A^TA)^-1 have far-reaching implications in linear algebra.

2) Calculus solution – find the minimum error

E² = |A – b|²

            dE²/x = 2A^TAx – 2A^Tb = 0

A^TAx = A^Tb   

 = (A^TA)^-1A^Tb

3) Perpendicularity- Error vector must be perpendicular to every column vector in A

            a₁^T(b – A) =  0

                        …

            a_n^T(b – A) = 0

or

            A^T(b – A) = 0

or

            A^TA = A^Tb

 = (A^TA)^-1A^Tb

4) Vector subspaces – Vectors perpendicular to column space lie in left null space

    i.e., the error vector b – A must be in the null space of A^T

            A^T(b – A) = 0

            A^TA = A^Tb

 = (A^TA)^-1A^Tb

Multi-Variable Projection Matrices

In the language of linear algebra, if b is not in the column space of A then Ax=b cannot be solved exactly since Ax can never leave the column space. The solution is to make the error vector Ax-b small, i.e., choose the closest point to b in the column space. This point is the projection of b into the column space of A.

When m > n the least-squares solution for column vector x in Ax = b is given by

 = (A^TA)^-1A^Tb

Transforming  by matrix A yields

            p = A = {A(A^TA)^-1A^T}b

which in matrix terms expresses the construction of a perpendicular line from vector b into the column space of A. The projection operator P is given by

            P =  A(A^TA)^-1A^T

Note the analogy with the single-variable case with projection operator. In both cases, p = Pb is the component of b projected into the column space of A.

E = b – Pb is the orthogonal error vector.

Aside: If you want to stretch your imagination, recall the SVD factorization yields V, the eigenvectors of A^TA, which are the axes of the error ellipsoid. The singular values are the lengths of the corresponding axes.

In orbit control, the projection operator takes orbits into orbits.

 = Rq = R(R^TR)^-1R^Tx

 (R^TR)^-1R^T is a column vector of correctors, q.

MATLAB Example – Projection of a vector into a subspace (least-squares)

>>edit lsq_2

Under-Constrained Problems  (Right Pseudoinverse)

Noting that (AA^T)(A^TA)^-1=I we can write Ax=b in the form

            Ax = (AA^T)(A^TA)^-1b

or

            x = (A^T)(A^TA)^-1b = A⁺b

where A⁺b is the right pseudoinverse of  matrix A.

MATLAB Example – Underconstrained least-squares (pseudoinverse)

>>edit lsq_3

Weighted Least Squares

When individual measurements carry more or less weight, the individual rows of Ax=b can be multiplied by weighting factors.

In matrix form, weighted-least-squares looks like

            W(Ax) = W(b)

where W is a diagonal matrix with the weighting factors on the diagonal. Proceeding as before,

            (WA)^T(WA)x = (WA)^TWb

            x = ((WA)^T(WA))^-1 (WA)^TWb

When the weighting matrix W is the identity matrix, the equation collapses to the original solution x = (A^TA)^-1A^Tb.

In orbit correction problems, row weighting can be used to emphasize or de-emphasize specific BPMS. Column weighting can be used to emphasize or de-emphasize specific corrector magnets. In response matrix analysis the individual BPM readings have different noise factors (weights).

Orbit Correction Using Least-Squares

Consider the case of orbit correction using more BPMS than corrector magnets.

x = Rq          or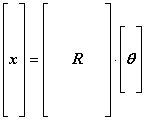

x = orbit (BPM)/constraint column vector (mm)

q = corrector/variable column vector (ampere or mrad)

R = response matrix (mm/amp or mm/mrad)

In this case, there are more variables than constraints (the response matrix R has m>n). Using a graphical representation to demonstrate matrix dimensionality, the steps required to find a least squares solution are 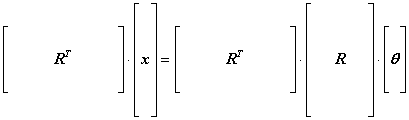 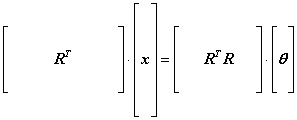                                 (normal equations)

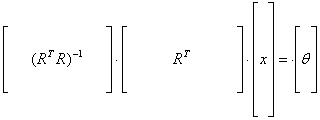
or

q= (R^TR)^-1R^Tx

The projection operator predicts the orbit from corrector set q:

= R(R^TR)^-1R^Tx

and the orbit error is

e= x –  = (I - R(R^TR)^-1R^T)x

Note that in order to correct the orbit, we reverse the sign of q before applying the solution to the accelerator. You will not be the first or last person to get the sign wrong.

            Feynman’s rule:   ‘If the sign is wrong, change it’.

MATLAB Example – Least-squares orbit correction

>>edit lsq_4

Response Matrix Analysis Example

Response matrix analysis linearizes an otherwise non-linear problem and iterates to find the solution. The linearization process amounts to a Taylor series expansion to first order. For a total of l quadrupole strength errors the response matrix expansion is

where the measured response matrix R has dimensions m x n and all of {R₀, dR_o/dk_j} are calculated numerically. To set up the Ax=b problem, the elements of the coefficient matrix A contain numerical derivatives dR^ij/dk_l. The constraint vector b has length m times n and contains terms from R-R₀. The variable vector x has length l and contains the Taylor expansion terms Dk₁,…Dk_l. The matrix mechanics looks like

The 'chi-square' fit quality factor is

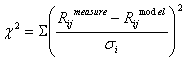
where  is the rms measurement error associated with the i^th BPM.

SVD and Least-Squares

The least-squares solution to Ax=b where m>n is given by

            x_lsq= (A^TA) ^-1A^Tb

Singular value decomposition of A yields

            A = UWV^T.

Using the  pseudoinverse,

            A⁺=VW^-1U^T

leads to

            x_svd = A⁺b = VW^-1U^T*b

Does x_lsq= x_svd for over-constrained problems m > n?

Exercise: analytically substitute the singular value decomposition expressions for A and A^T to show

            (A^TA) ^-1A = VW^-1U^T.

Hence, SVD recovers the least-squares solution for an over-constrained system of equations.

Home page of Orbit Movement and Beam Position Control