

Next: References
Up: Introduction to Object-Oriented Programming
Previous: 9 More on C++
Subsections
In C++ generic data types are called class templates![[*]](foot_motif.gif) or just templates
for short.
A class template looks like a normal class
definition, where some aspects are represented by placeholders. In the
forthcoming list example we use this mechanism to generate lists for various
data types:
or just templates
for short.
A class template looks like a normal class
definition, where some aspects are represented by placeholders. In the
forthcoming list example we use this mechanism to generate lists for various
data types:
template <class T>
class List : ... {
public:
...
void append(const T data);
...
};
In the first line we introduce the keyword template which starts every
template declaration. The arguments of a template are enclosed in angle
brackets.
Each argument specifies a placeholder in the following class definition. In
our example, we want class List to be defined for various data types.
One could say, that we want to define a class of lists![[*]](foot_motif.gif) . In this case the class of lists is
defined by the type of
objects they contain. We use the name T for the placeholder. We now use
T at any place where normally the type of the actual objects are
expected.
For example, each list provides a method to append an element to it. We can
now define this method as shown above with use of T.
. In this case the class of lists is
defined by the type of
objects they contain. We use the name T for the placeholder. We now use
T at any place where normally the type of the actual objects are
expected.
For example, each list provides a method to append an element to it. We can
now define this method as shown above with use of T.
An actual list definition must now specify the type of the list. If we
stick to the class expression used before, we have to create a class
instance. From this class instance we can then create ``real'' object
instances:
List<int> integerList;
Here we create a class instance of a List which takes integers as its
data elements. We specify the type enclosed in angle brackets. The compiler
now applies the provided argument ``int'' and automatically generates a class
definition where the placeholder T is replaced by int, for
example, it generates the following method declaration for append():
void append(const int data);
Templates can take more than one argument to provide more placeholders. For
example, to declare a dictionary class which provides access to its data
elements by a key, one can think of the following declaration:
template <class K, class T>
class Dictionary {
...
public:
...
K getKey(const T from);
T getData(const K key);
...
};
Here we use two placeholders to be able to use dictionaries for various key
and data types.
Template arguments can also be used to generate parameterized class
definitions. For example, a stack might be implemented by an array of data
elements. The size of the array could be specified dynamically:
template <class T, int size>
class Stack {
T _store[size];
public:
...
};
Stack<int,128> mystack;
In this example, mystack is a stack of integers using an array of 128
elements. However, in the following we will not use parameterized classes.
In the following discussion we distinguish between a data structure's
shape and its traversing strategies. The first is the ``look'', which
already provides plenty information about the building blocks of the
data structure.
A traversing strategy defines the order in which elements of the
data structure are to be visited. It makes sense
to separate the shape from
traversing strategies, because some data structures can be traversed using
various strategies.
Traversing of a data structure is implemented using iterators.
Iterators guarantee to visit each data item of their associated data
structure in a well defined order. They must provide at least the following
properties:
- 1.
- Current element. The iterator visits data elements one at
a time. The element which is currently visited is called ``current
element''.
- 2.
- Successor function. The execution of the step to the next
data element depends on the traversing strategy implemented by the
iterator. The ``successor function'' is used to return the
element which is next to be visited: It returns the successor of the
current element.
- 3.
- Termination condition. The iterator must provide a
mechanism to check whether all elements are visited or not.
When doing something object-oriented, the first question to ask is
What are the basic building blocks of the item to implement?
Have a look at Figure 10.1, which shows a list consisting of four
rectangles.
Each rectangle has a bullet in its middle, the first three point to their
right neighbour. Since the last rectangle have no right neighbour, there is no
pointer.
Figure 10.1:
Basic building blocks of a singly linked list.
 |
First let's choose names for these building blocks. Talking of rectangles
is not appropriate, because one can think of a figure using circles or
triangles.
Within the scope of graphs the name node is used. A
node contains a pointer to its successor. Thus, the list
in the figure consists of nodes, each of which has
exactly one pointer associated with it.
Three types of nodes can be distinguished:
- The first node (head), which has no predecessor,
- the middle nodes, which have exactly one predecessor and
exactly one successor and
- the last node (tail), which has no successor.
Note that the nodes do not carry any content. This is because the bare
data structure list consists only of nodes, which are strung together.
Of course real applications need nodes, carrying some content. But in the
sense of object-orientation this is a specialization of the nodes.
From the figure we can see, that
a list can only be used with one
traversing strategy: forward cursor. Initially, the head will be the
first current element. The successor function simply follows the pointer
of the current node. The termination function checks the
current element to be the tail.
Note that it is not possible to go back nor to start in the middle of
the list. The latter would contradict the requirement, that each element must
be visited.
The next question is, what are the operations offered by a list? A list
only defines two well known nodes head and tail. Let's have a
deeper look to them.
A new node can be put-in-front of the list such that:
- its pointer is set to the current head,
- the new node becomes the new head.
Similarly, a new node can easily be appended to the tail:
- the tail pointer is set to the new node,
- the new node becomes the new tail.
The inverse function to put in front is delete-from-front:
- the successor node of the head becomes the new head,
- the formerly head node is discarded.
You should be able to figure out why there is no cheap inverse append
function.
Finally, there exist three other cheap primitives, whose meaning is
straight forward. Thus, we will not examine them
any further. However, we present them here for completeness:
- get-first: returns the (data of the) head node,
- get-last: returns the (data of the) tail node and
- is-empty: returns whether the list is empty or not.
The basic building block of a list is the node. Thus, let's first
declare a class for it. A node has nothing
more than a pointer to another node. Let's assume, that this neighbour is
always on the right side.
Have a look at the following declaration of class Node.
class Node {
Node *_right;
public:
Node(Node *right = NULL) : _right(right) {}
Node(const Node &val) : _right(val._right) {}
const Node *right() const { return _right; }
Node *&right() { return _right; }
Node &operator =(const Node &val) {
_right = val._right;
return *this;
}
const int operator ==(const Node &val) const {
return _right == val._right;
}
const int operator !=(const Node &val) const {
return !(*this == val);
}
};
A look to the first version of method right() contains a const
just before the method body. When used in this position, const declares
the method to be constant regarding the elements of the invoking object.
Consequently, you are only allowed to use this mechanism in method
declarations or definitions, respectively.
This type of const modifier is also used to check for overloading. Thus,
class Foo {
...
int foo() const;
int foo();
};
declare two different methods. The former is used in constant contexts whereas
the second is used in variable contexts.
Although template class Node implements a simple node it seems to define
plenty of functionality. We do this, because it is good practice to offer at
least the following functionality for each defined data type:
- Copy Constructor. The copy constructor is needed to allow
definition of objects which are initialized from already existing
ones.
- operator =. Each object should know how to assign other
objects (of the same type) to itself. In our example class, this is
simply the pointer assignment.
- operator ==. Each object should know how to compare itself
with another object.
The unequality operator ``!='' is implemented by using the definition of the
equality operator. Recall, that this points to the invoking object, thus,
Node a, b;
...
if (a != b) ...
would result in a call to operator !=() with this set to the
address of a. We dereference this using the standard dereference
operator ``*''. Now, *this is an object of class Node which is
compared to another object using operator ==(). Consequently, the
definition of operator ==() of class Node is used. Using the
standard boolean NOT operator ``!'' we negate the result and obtain the truth
value of operator !=().
The above methods should be available for each class you define. This ensures
that you can use your objects as you would use any other objects, for example
integers. If some of these methods make no sense for whatever reason, you
should declare them in a private section of the class to explicitly mark them
as not for public use. Otherwise the C++ compiler would substitute standard
operators.
Obviously, real applications require the nodes to carry data. As mentioned
above, this means to specialize the nodes. Data can be of any type, hence, we
are using the template construct.
template <class T>
class DataNode : public Node {
T _data;
public:
DataNode(const T data, DataNode *right = NULL) :
Node(right), _data(data) {}
DataNode(const DataNode &val) :
Node(val), _data(val._data) {}
const DataNode *right() const {
return((DataNode *) Node::right());
}
DataNode *&right() { return((DataNode *&) Node::right()); }
const T &data() const { return _data; }
T &data() { return _data; }
DataNode &operator =(const DataNode &val) {
Node::operator =(val);
_data = val._data;
return *this;
}
const int operator ==(const DataNode &val) const {
return(
Node::operator ==(val) &&
_data == val._data);
}
const int operator !=(const DataNode &val) const {
return !(*this == val);
}
};
The above template DataNode simply specializes class Node to carry
data of any type. It adds functionality to access its data element and also
offers the same set of standard functionality: Copy Constructor,
operator =() and operator ==(). Note, how we reuse functionality
already defined by class Node.
Now
we are able to declare the list template. We also use the template mechanism
here, because we want the list to carry data of
arbitrary type. For example, we want to be able
to define a list of integers. We start with an abstract class template
ListBase which functions as the base class of all other lists. For example,
doubly linked lists obviously share the same properties like singly linked
lists.
template <class T>
class ListBase {
public:
virtual ~ListBase() {} // Force destructor to be
// virtual
virtual void flush() = 0;
virtual void putInFront(const T data) = 0;
virtual void append(const T data) = 0;
virtual void delFromFront() = 0;
virtual const T &getFirst() const = 0;
virtual T &getFirst() = 0;
virtual const T &getLast() const = 0;
virtual T &getLast() = 0;
virtual const int isEmpty() const = 0;
};
What we actually do is to describe the interface of every list by specifying
the prototypes of required methods. We do that for every operation we have
identified in section 10.3. Additionally, we also include a
method flush() which allows us to delete all elements of a list.
For operations get-first and get-last we have declared two
versions. One is for use in a constant context and the other in a variable
context.
With this abstract class template we are able to actually define our list
class template:
template <class T>
class List : public ListBase<T> {
DataNode<T> *_head, *_tail;
public:
List() : _head(NULL), _tail(NULL) {}
List(const List &val) : _head(NULL), _tail(NULL) {
*this = val;
}
virtual ~List() { flush(); }
virtual void flush();
virtual void putInFront(const T data);
virtual void append(const T data);
virtual void delFromFront();
virtual const T &getFirst() const { return _head->data(); }
virtual T &getFirst() { return _head->data(); }
virtual const T &getLast() const { return _tail->data(); }
virtual T &getLast() { return _tail->data(); }
virtual const int isEmpty() const { return _head == NULL; }
List &operator =(const List &val) {
flush();
DataNode<T> *walkp = val._head;
while (walkp) append(walkp->data());
return *this;
}
const int operator ==(const List &val) const {
if (isEmpty() && val.isEmpty()) return 1;
DataNode<T> *thisp = _head,
*valp = val._head;
while (thisp && valp) {
if (thisp->data() != valp->data()) return 0;
thisp = thisp->right();
valp = valp->right();
}
return 1;
}
const int operator !=(const List &val) const {
return !(*this == val);
}
friend class ListIterator<T>;
};
The constructors initialize the list's elements _head and _tail
to NULL which is the NUL pointer in C and C++.
You should know how to implement the other methods from your
programming experience. Here we only present the implementation of method
putInFront():
template <class T> void
List<T>::putInFront(const T data) {
_head = new DataNode<T>(data, _head);
if (!_tail) _tail = _head;
} /* putInFront */
If we define methods of a class template outside of its declaration, we must
also specify the template keyword. Again we use the new operator
to create a new data node dynamically. This operator allows initialization of
its created object with arguments enclosed in parenthesis. In the above
example, new creates a new instance of class DataNode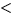 T
T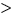 .
Consequently, the corresponding constructor is called.
.
Consequently, the corresponding constructor is called.
Also notice how we use placeholder T. If we would create a class
instance of class template List, say, List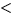 int
int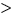 this would
also cause creation of a class instance of class template DataNode, viz
DataNode
this would
also cause creation of a class instance of class template DataNode, viz
DataNode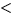 int
int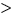 .
.
The last line of the class template declaration declares
class template ListIterator to be a friend of List. We want to
separately define the list's iterator. However, it is closely related, thus,
we allow it to be a friend.
In section 10.2 we have introduced the concept of
iterators
to traverse through a data structure. Iterators must implement three
properties:
- Current element.
- Successor function.
- Termination condition.
Generally speaking, the iterator successively returns data associated with the
current element. Obviously, there will be a method, say, current() which
implements this functionality. The return type of this method depends on the
type of data
stored in the particular data structure. For example, when iterating over
List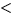 int
int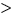 the return type should be int.
the return type should be int.
The successor function, say, succ(), uses additional information which
is stored in
structural elements of the data structure. In our list example, these are the
nodes which carry the data and a pointer to their right neighbour. The
type of the structural elements usually differs from that of the raw data.
Consider again our List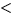 int
int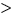 where succ() must use
DataNode
where succ() must use
DataNode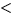 int
int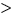 as structural elements.
as structural elements.
The termination condition is implemented by a method, say, terminate(),
which returns TRUE if (and only if) all data elements of the associated
data structure have been visited. As long as succ() can find an element
not yet visited, this method returns FALSE.
Again we want to specify an abstract iterator class which defines properties
of every iterator. The thoughts above lead to the following declaration:
template <class Data, class Element>
class Iterator {
protected:
Element _start,
_current;
public:
Iterator(const Element start) :
_start(start), _current(start) {}
Iterator(const Iterator &val) :
_start(val._start), _current(val._current) {}
virtual ~Iterator() {}
virtual const Data current() const = 0;
virtual void succ() = 0;
virtual const int terminate() const = 0;
virtual void rewind() { _current = _start; }
Iterator &operator =(const Iterator &val) {
_start = val._start;
_current = val._current;
return *this;
}
const int operator ==(const Iterator &val) const {
return(_start == val._start && _current == val._current);
}
const int operator !=(const Iterator &val) const {
return !(*this == val);
}
};
Again we use the template mechanism to allow the use of the iterator
for any data structure which stores data of type Data and which
uses structural elements of type Element. Each iterator ``knows''
a starting (structural) element and the current element. We make both
accessible from derived classes because derived iterators need access
to them to implement the following iterator properties. You should
already understand how the constructors operate and why we force
the destructor to be virtual.
Subsequently we specify three methods which should implement the three
properties of an iterator. We also add a method rewind() which
simply sets the current element to the start element. However,
complex data structures (for example hash tables) might require more
sophisticated rewind algorithms. For that reason we also specify this
method to be virtual, allowing derived iterators to redefine
it for their associated data structure.
The last step in the iterator implementation process is the declaration
of the list iterator. This iterator is highly related to our class
template List, for example, it is clear that the structural
elements are class templates DataNode. The only ``open'' type is
the one for the data. Once again, we use the template mechanism to
provide list iterators for the different list types:
template <class T>
class ListIterator : public Iterator<T, DataNode<T> *> {
public:
ListIterator(const List<T> &list) :
Iterator<T, DataNode<T> *>(list._head) {}
ListIterator(const ListIterator &val) :
Iterator<T, DataNode<T> *>(val) {}
virtual const T current() const { return _current->data(); }
virtual void succ() { _current = _current->right(); }
virtual const int terminate() const {
return _current == NULL;
}
T &operator ++(int) {
T &tmp = _current->data();
succ();
return tmp;
}
ListIterator &operator =(const ListIterator &val) {
Iterator<T, DataNode<T> *>::operator =(val);
return *this;
}
};
The class template ListIterator is derived from Iterator. The type
of data is, of course, the type for which the list iterator is declared,
hence, we insert placeholder T for the iterator's data type Data.
The iteration process is achieved with help of the structural elements of type
DataNode. Obviously the starting element is the head of the list
_head which is of type DataNode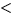 T
T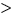 *. We choose this type for the
element type Element.
*. We choose this type for the
element type Element.
Note that the list iterator actually hides the details about the structural
elements. This type highly depends on the implementation of the list. For
example, if we would have chosen an array implementation, we may have used
integers as structural elements where the current element is indicated by an
array index.
The first constructor takes the list to traverse as its argument and
initializes its iterator portion accordingly. As each
ListIterator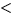 T
T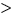 is a friend of List
is a friend of List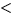 T
T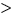 it has access to the
list's private members. We use this to initialize the iterator to point to the
head of the list.
it has access to the
list's private members. We use this to initialize the iterator to point to the
head of the list.
We omit the destructor because we do not have any additional data members for
the list iterator. Consequently, we do nothing special for it. However, the
destructor of class template Iterator is called. Recall that we have to
define this destructor to force derived classes to also have a virtual one.
The next methods just define the required three properties. Now that we have
structural elements defined as DataNode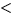 T
T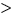 * we use them as follows:
* we use them as follows:
- the current element is the data carried by the current
structural element,
- the successor function is to set the current structural
element to its right neighbour and
- the termination condition is to check the current structural
element if it is the NULL pointer. Note that this can happen
only in two cases:
- 1.
- The list is empty. In this case the current element is
already NULL because the list's head _head is
NULL.
- 2.
- The current element reached the last element. In this
case the previous successor function call set the current
element to the right neighbour of the last element which is
NULL.
We have also included an overloaded postincrement operator ``++''. To
distinguish this operator from the preincrement operator, it takes an
additional (anonymous) integer argument. As we only use this argument to
declare a correct
operator prototype and because we do not use the value of the argument, we
omit the name of the argument.
The last method is the overloaded assignment operator for list
iterators. Similar to previous assignment operators, we just reuse already
defined assignments of superclasses; Iterator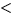 T
T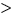 ::operator =() in
this case.
::operator =() in
this case.
The other methods and operators, namely rewind(), operator ==()
and operator !=() are all inherited from class template Iterator.
The list template as introduced in previous sections can be used as follows:
int
main() {
List<int> list;
int ix;
for (ix = 0; ix < 10; ix++) list.append(ix);
ListIterator<int> iter(list);
while (!iter.terminate()) {
printf("%d ", iter.current());
iter.succ();
}
puts("");
return 0;
}
As we have defined a postincrement operator for the list iterator, the loop
can also be written as:
while (!iter.terminate())
print("%d ", iter++);
The presented example focusses on an object-oriented view. In real
applications singly linked lists might offer more functionality. For example,
insertion of new data items should be no problem due to the use of pointers:
- 1.
- Take the successor pointer of the new element and set it
to the element which should become its right neighbour,
- 2.
- Take the successor pointer of the element after which the
new element should be inserted and set it to the new element.
Two simple operations. However, the problem is to designate the element after
which the new element should be inserted. Again, a mechanism is needed which
traverse through the list. This time, however, traversion stops at a
particular element: It is the element where the list (or the data structure)
is modified.
Similar to the existence of different traversing strategies, one can think of
different modification strategies. For example, to create a sorted list,
where elements are sorted in ascending order, use an ascending modifier.
These modifiers must have access to the list structural elements, and thus,
they would be declared as friends as well. This would lead to the necessity
that every modifier must be a friend of its data structure. But who can
guarantee, that no modifier is forgotten?
A solution is, that modification strategies are not implemented by
``external'' classes as iterators are. Instead, they are implemented by
inheritance. If a sorted list is needed, it is a specialization of the general
list. This sorted list would add a method, say insert(), which inserts a
new element according to the modification strategy.
To make this possible, the presented list template must be changed. Because
now, derived classes must have access to the head and tail node to implement
these strategies. Consequently, _head and _tail should
be protected.
The presented iterator implementation assumes, that the data structure is not
changed during the use of an iterator. Consider the following example to
illustrate this:
List<int> ilist;
int ix;
for (ix = 1; ix < 10; ix++)
ilist.append(ix);
ListIterator<int> iter(ilist);
while (!iter.terminate()) {
printf("%d ", iter.current());
iter.succ();
}
printf("\n");
ilist.putInFront(0);
iter.rewind();
while (!iter.terminate()) {
printf("%d ", iter.current());
iter.succ();
}
printf("\n");
This code fragment prints
1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9
instead of
1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
This is due to the fact, that our list iterator only stores pointers to
the list structural elements. Thus, the start element _start is
initially set to point to the location where the list's head node _head
points to. This simply leads to two different pointers referencing the
same location. Consequently, when changing one pointer as it is done by
invoking putInFront() the other pointer is not affected.
For that reason, when rewinding the iterator after putInFront() the
current element is set to the start element which was set at the time the
iterator constructor was called. Now, the start element actually references
the second element of the list.
- 1.
- Similar to the definition of the postincrement operator in
class template ListIterator, one
could define a preincrement operator as:
T &operator ++() {
succ();
return _current->data();
}
What problems occur?
- 2.
- Add the following method
int remove(const T &data);
to class template List. The method should delete the first
occurrence of data in the list. The method should return 1 if it
removed an element or 0 (zero) otherwise.
What functionality must data provide? Remember that it
can be of any type, especially user defined classes!
- 3.
- Derive a class template CountedList from List which
counts its elements. Add a method count() of arbitrary type
which returns the actual number of elements stored in the list. Try to
reuse as much of List as possible.
- 4.
- Regarding the iterator problem discussed in
section 10.7. What are possible solutions to allow the
list to be altered while an iterator of it is in use?


Next: References
Up: Introduction to Object-Oriented Programming
Previous: 9 More on C++
P. Mueller
8/31/1997
![[*]](foot_motif.gif) . In this case the class of lists is
defined by the type of
objects they contain. We use the name T for the placeholder. We now use
T at any place where normally the type of the actual objects are
expected.
For example, each list provides a method to append an element to it. We can
now define this method as shown above with use of T.
. In this case the class of lists is
defined by the type of
objects they contain. We use the name T for the placeholder. We now use
T at any place where normally the type of the actual objects are
expected.
For example, each list provides a method to append an element to it. We can
now define this method as shown above with use of T.
